2019-06-27 • 强化学习

CHAPTER 7. n-step Bootstrapping

本章将统一 MC 和 one-step TD.

7.1 $n$-step TD Prediction

n-step TD 方法介于 MC 与 one-step TD 之间，使用一个 episode 中的多个立即奖励作为依据进行更新。

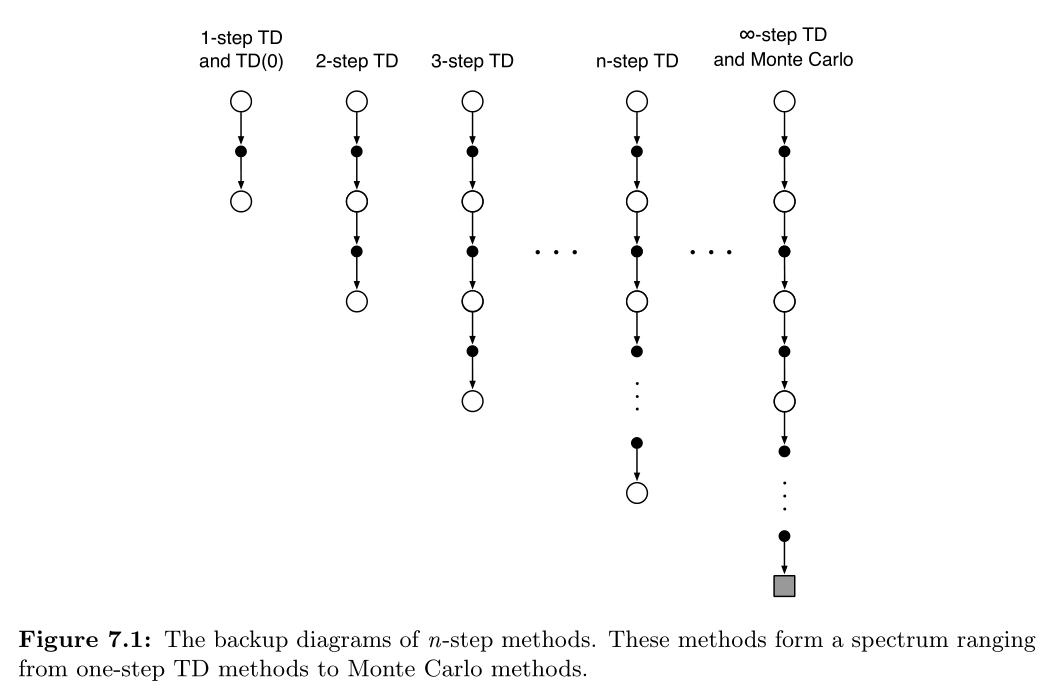
figure_7_1

更新时使用的 target 是 n-step return:

$G_{t:t+n}\doteq R_{t+1}+\gamma R_{t+1}+\dots +\gamma^{n-1}R_{t+n}+\gamma^nV_{t+n-1}(S_{t+n}) \tag{7.1}$

简单的更新规则为：

$V_{t+n}(S_t)\doteq V_{t+n-1}(S_t)+\alpha \big[G_{t:t+n}-V_{t+n-1}(S_t)\big] \tag{7.2}$

单纯的 n-step TD ：

figure_7_1_

使用值函数 $V_{t+n-1}$ 来校正 $R_{t+n}$ 之后的奖励值。
可以保证的是，在最坏情形下，它们的期望值会比 $V_{t+n-1}$ 更贴近于 $v_\pi$.

$\max_s \big|\mathbb E_\pi[G_{t:t+n}|S_t=s]-v_\pi(s)\big|\leq \gamma^n \max_s \big|V_{t+n-1}(s)-v_\pi(s)\big| \tag{7.3}$

这叫做 n-step returns 的 error reduction property .
由该特性，可以正式表明所有的 n-step TD 方法，在适当的技巧下，都能收敛到准确的预测。
由此可以得出一系列合理的方法，包括 one-step TD 与 MC 都是 n-step TD 的极端形式。

Example 7.1： n-step TD Methods on the Random Walk

假设第一个 episode 从 C 开始，一路向右经过 D，E，最后终结得到奖励 1.
回到那些开始于中间状态的估计值，$V(s)=0.5$.
对于 one-step TD，只有 $V(E)$ 会更新为 1，其余都不变。
而 two-step TD，就是 $V(D)=V(E)=1$. 如果是 3-step TD，则 C 的估计值也会变为 1.

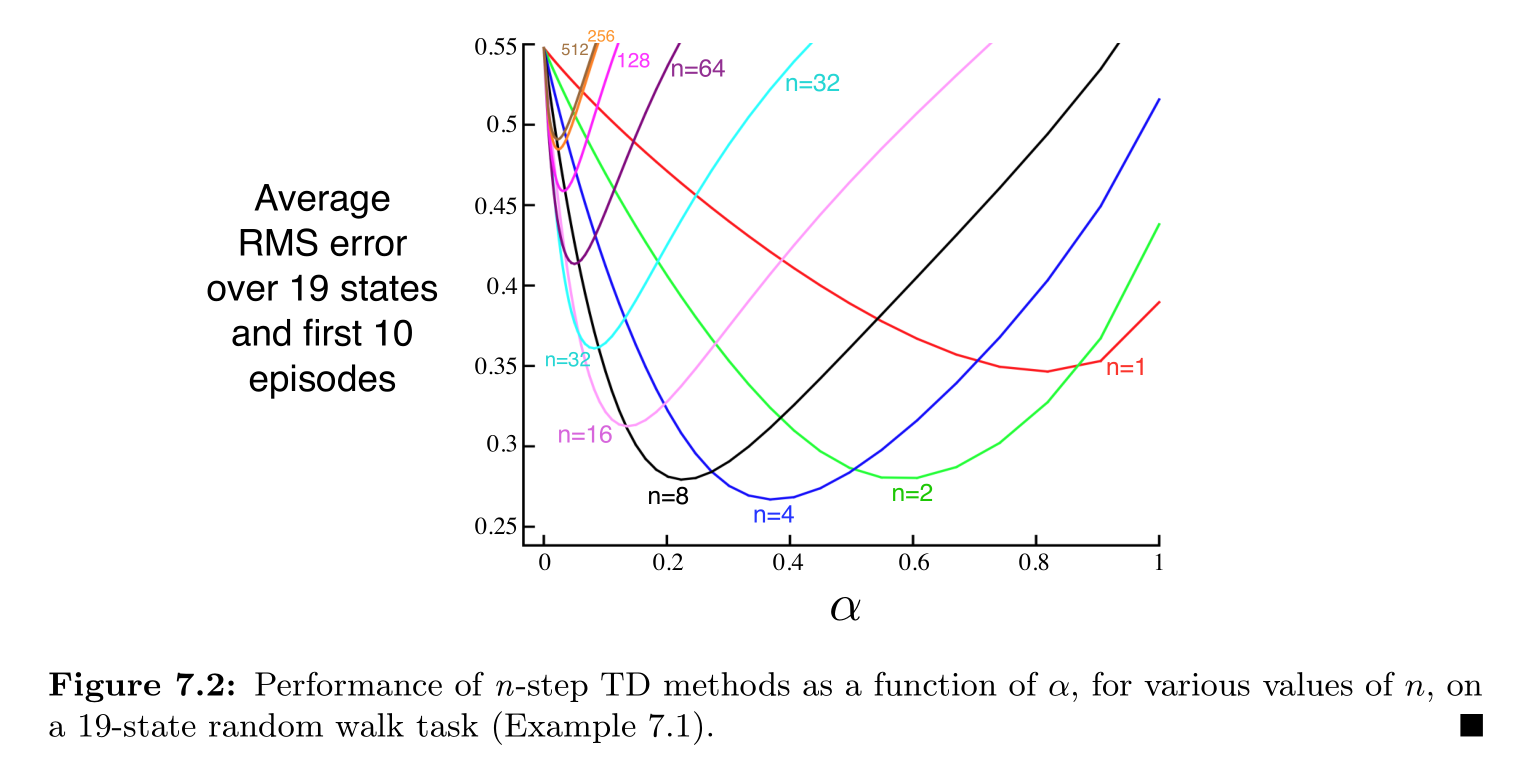
figure_7_2

从上图可以看出，n 的值适中对性能的提升是巨大的，两种极端情况—MC 和 one-step TD 的性能都不是最佳的。

7.2 $n$-step Sarsa

将 n-step 用到 Sarsa 的主要思想是：把 states 换成 actions(或 state-action pairs)，然后使用一个 $\epsilon$-greedy policy.
backup diagram 与 n-step TD 没有多大区别：

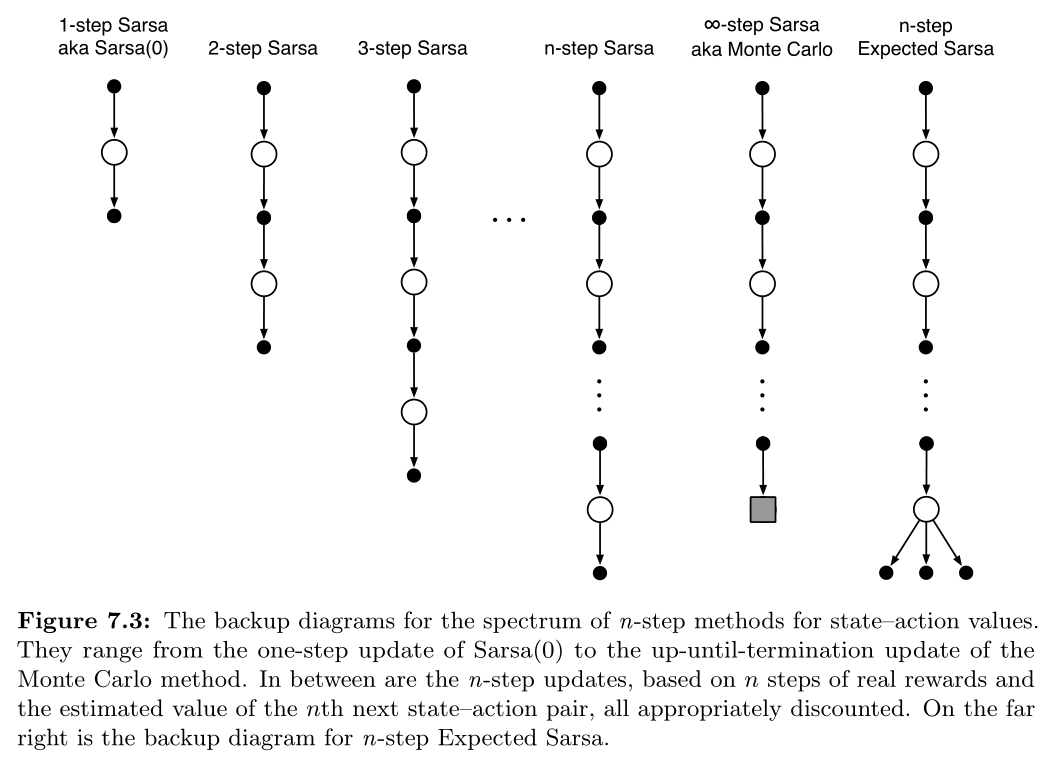
figure_7_3

n-step returns 也要重新定义一下：

$G_{t:t+n}\doteq R_{t+1}+\gamma R_{t+1}+\dots +\gamma^{n-1}R_{t+n}+\gamma^nQ_{t+n-1}(S_{t+n},A_{t+n}),\qquad n\geq 1,\quad 0\leq t<T-n. \tag{7.4}$

更新规则：

$Q_{t+n}(S_t,A_t)\doteq Q_{t+n-1}(S_t,A_t)+\alpha \big[G_{t:t+n}-Q_{t+n-1}(S_t,A_t)\big], \qquad 0\leq t<T, \tag{7.5}$

伪代码：

figure_7_2_

网格例子：

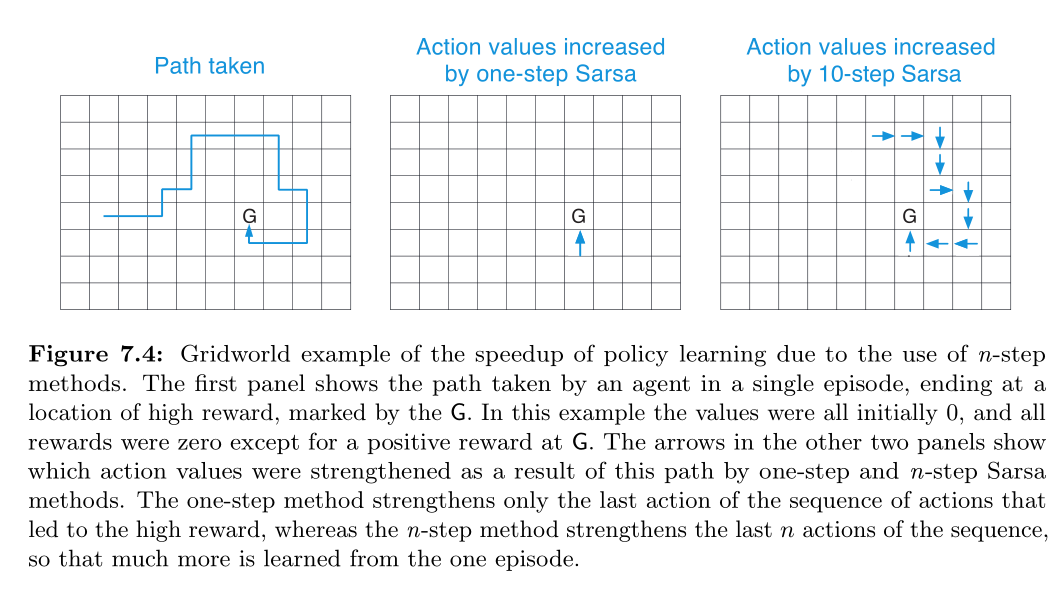
figure_7_4

对于 Expected Sarsa，仅在最后将估计值替换为期望即可：

$G_{t:t+n}\doteq R_{t+1}+\gamma R_{t+1}+\dots +\gamma^{n-1}R_{t+n}+\gamma^n\bar V_{t+n-1}(S_{t+n}),\qquad t+n<T, \tag{7.7}$

其中 $\bar V_t(s)$ 叫状态 s 的 expected approximate value，

$\bar V_t(s)\doteq \sum_a\pi(a|s)Q_t(s,a),\quad for\ all\ s\in \mathcal S. \tag{7.8}$

7.3 $n$-step Off-policy Learning

在 off-policy 方法中，关键还是两个不同策略的重要性采样系数 $\rho$ ，区别只在于它用了 n 个动作而已。

$V_{t+n}(S_t) \doteq V_{t+n-1}(S_t)+ \alpha \rho_{t:t+n-1} \big[G_{t:t+n}-V_{t+n-1}(S_t)\big], \quad 0 \leq t< T \tag{7.9}$

其中 $\rho_{t:h}\doteq \prod_{k=t}^{min(h,T-1)}\frac{\pi(A_k|S_k)}{b(A_k|S_k)} \tag{7.10}$
而对于使用 state-action value function 的算法，可以用同样的办法调整公式，使之变成 off-policy 方法。

$Q_{t+n}(S_t,A_t)\doteq Q_{t+n-1}(S_t,A_t)+\alpha \rho_{t+1:t+n}\big[G_{t:t+n}-Q_{t+n-1}(S_t,A_t)\big], \quad for\ 0\leq t<T \tag{7.11}$

这里有个小差别，就是 $\rho$ 的起止向后移了一步；这是因为在 t 时刻，我们已经选择了 $A_t$，那么后面就不需要关心 $A_t$ ，而关注于其后的 n 个动作。

对于 n-step Expected Sarsa 的 off-policy 版本，与 n-step Sarsa 类似，区别仅在于重要采样率会少一个参考量： $\rho_{t+1:t+n-1}$ 变成 $\rho_{t+1:t+n-2}$. 当然回报值也会变成期望版本。

off_policy_n_step_sarsa

7.4 *Per-decision Off-policy Methods with Control Variates

以上所介绍的 multi-step off-policy 方法简单明了，但效率并不高。
一种更为复杂的方法，使用了 per-decision importance sampling，就如在章节 5.9 介绍那样：
原始的 n-step 回报可以写做：

$G_{t:h}=R_{t+1}+\gamma G_{t+1:h}, \qquad t<h<T, \tag{7.12}$

其中 $G_{h:h}\doteq V_{h-1}(S_h).$
当使用 off-policy 方法，即行为策略与目标策略不同时，需要添加权重 $\rho_t=\frac{\pi(A_t|S_t)}{b(A_s|S_t)}$.
最简单的方法就是直接在上式右侧乘上该权重，但是在某些情况下，比如 $\rho_t=0$ 也就是目标策略 $\pi$ 选中该动作的概率为 0 时，$G_{t:h}$ 会整个变成 0.
当以这个 0 作为 target 更新值时，会带来非常大的变动，这和上一节的变化是不一样的。
可以用一个略微复杂的式子来对值进行更新，off-policy definition of the n-step return：

$G_{t:h}\doteq \rho_t(R_{t+1}+\gamma G_{t+1:h})+(1-\rho_t)V_{h-1}(S_t),\qquad t<h<T, \tag{7.13}$

上式中多出来的部份叫做控制变量(control variate)，它并不改变期望值，$\rho$ 的期望值是 1，且与估计值无关，所以控制变量的期望是 0.
另外，上式与 on-policy 的式子其实是一致的，即 $\rho_t$ 恒等于 1 时。
对于传统的 n-step 方法，与上式一起使用的学习规则是 n-step TD update (7.2)，除了回报中内嵌的 $\rho$ 外，没有显式的重要性采样率。
对于 action values，因为第一个动作在重要采样中并不起作用，所以 n-step return 的 off-policy 定义有一点不同。
第一个动作是已经被学习到的，即便在目标策略下，它不会被选中也不会造成什么影响，因为它已经被选中了，其后的 reward 和 state 权重必然是 1,.
首先 action values 的 n-step on-policy return 的期望形式 $(7.7)$，可以递归地写作 $(7.12)$，除了 action values 外，递归以 $G_{h:h+}\doteq \bar V_{h-1}(S_h)$ 结束，就如 $(7.8)$ 里一样。

使用控制变量的 off-policy 形式为：

$\begin{align} G_{t:h} & \doteq R_{t+1}+\gamma \Big(\rho_{t+1}G_{t+1:h}+\bar V_{h-1}(S_{t+1})-\rho_{t+1}Q_{h-1}(S_{t+1},A_{t+1})\Big),\\ & = R_{t+1}+\gamma \rho_{t+1}\Big(G_{t+1:h}-Q_{h-1}(S_{t+1},A_{t+1})\Big)+\gamma \bar V_{h-1}(S_{t+1}), \quad t< h \leq T. \tag{7.14} \end{align}$

如果 $h<T$，那么递归以 $G_{h:h}\doteq Q_{h-1}(S_h,A_h)$ 结束；如果 $h\geq T$，那么递归以 $G_{T-1:h}\doteq R_T.$ 结束。
最终的预测算法与 Expected Sarsa 类似。

重要采样率能够带来合适的 off-policy 方法，但是也造成了更新的方差过高，以至于必须使用很小的 step-size parameter 从而导致学习速度变慢。
off-policy 比 on-policy 慢可能是无法避免的，但是它们的性能是可以提升的。
控制变量是降低方差的有效方式，另一种方法是使 step sizes 快速适应观察到的方差，比如 Autostep method (Mahmood,Sutton,Degris and Pilarski,2012).

7.5 Off-policy Learning Without Importance Sampling: The $n$-step Tree Backup Algorithm

Tree-backup algorithm:

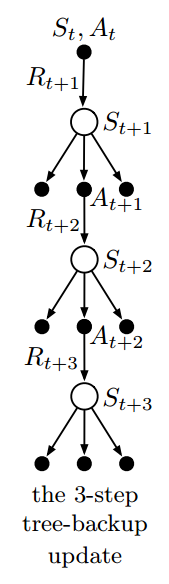
the_3-step_tree-backup_update

思想来于上图，之前的方法总是更新位于顶端节点的估计值(根据其下的奖励与底部节点的估计值)，使其靠近 target.
而在 tree-backup update 中，target 包括了图中的所有东西，包括悬于两旁的未被选中的动作。
更细致地讲，更新来自于叶子节点的动作估计值。而中间的实际选中的动作，并未参与更新。
每个叶子节点根据它在策略 $\pi$ 中出现的概率来调整权重参与更新。因此第一层的动作 $a$ 按照 $\pi(a|S_{t+1})$ 的权重参与更新。
除了实际选中的动作 $A_{t+1}$ 以外，因为它的概率 $\pi(A_{t+1}|S_{t+1})$ 用在了第二层的动作值的权重。
因此，每个未选中的第二层动作 $a’$ 的权重为 $\pi(A_{t+1}|S_{t+1})\pi(a’|S_{t+2})$
而每个第三层的动作的权重为 $\pi(A_{t+1}|S_{t+1})\pi(A_{t+2}|S_{t+2})\pi(a’‘|S_{t+3})$，依此类推。
这就好像图中每个指向动作节点的箭头都是被加权的，权重就是在目标策略下选中该动作的概率，而如果在该动作下有一棵树，那么该权重就会作用到这棵树下得所有叶子节点。

接下来将这个 3-step tree-backup update 看做由 6 个 half-steps，交替进行：从一个动作到下个状态的采样，以及从该状态考虑所有可能的动作及其在该策略下发生的可能性。
公式化描述如下，首先单步回报是与 Expected Sarsa 相同的：

$G_{t:t+1} \doteq R_{t+1}+\gamma \sum_a \pi(a|S_{t+1}) Q_t(S_{t+1},a), \qquad t< T-1$

而 tree-backup 的 two-step return ($t<T-2$)：

$\begin{align} G_{t:t+2} & \doteq R_{t+1}+\gamma \sum_{a \neq A_{t+1}} \pi(a|S_{t+1}) Q_t(S_{t+1},a) \\ & \qquad \qquad \quad +\gamma \pi(A_{t+1}|S_{t+1})\Big(R_{t+2}+\gamma \sum_a \pi(a|S_{t+2}) Q_{t+1}(S_{t+2},a)\Big) \\ & =R_{t+1}+\gamma \sum_{a\neq A_{t+1}}\pi(a|S_{t+1})Q_{t+1}(S_{t+1},a)+\gamma \pi(A_{t+1}|S_{t+1})G_{t+1:t+2}, \end{align}$

该回报作为 target 用于 n-step Sarsa 的更新：

$Q_{t+n}(S_t,A_t) \doteq Q_{t+n-1}(S_t,A_t)+\alpha [G_{t:t+n}-Q_{t+n-1}(S_t,A_t)]$

n-step_tree_backup_for_estimating

7.6 *A Unifying Algorithm $n$-step $Q(\sigma)$

本章介绍了三种不同的 action-value 算法，如图 7.5 的前三种 backup diagrams 所示：

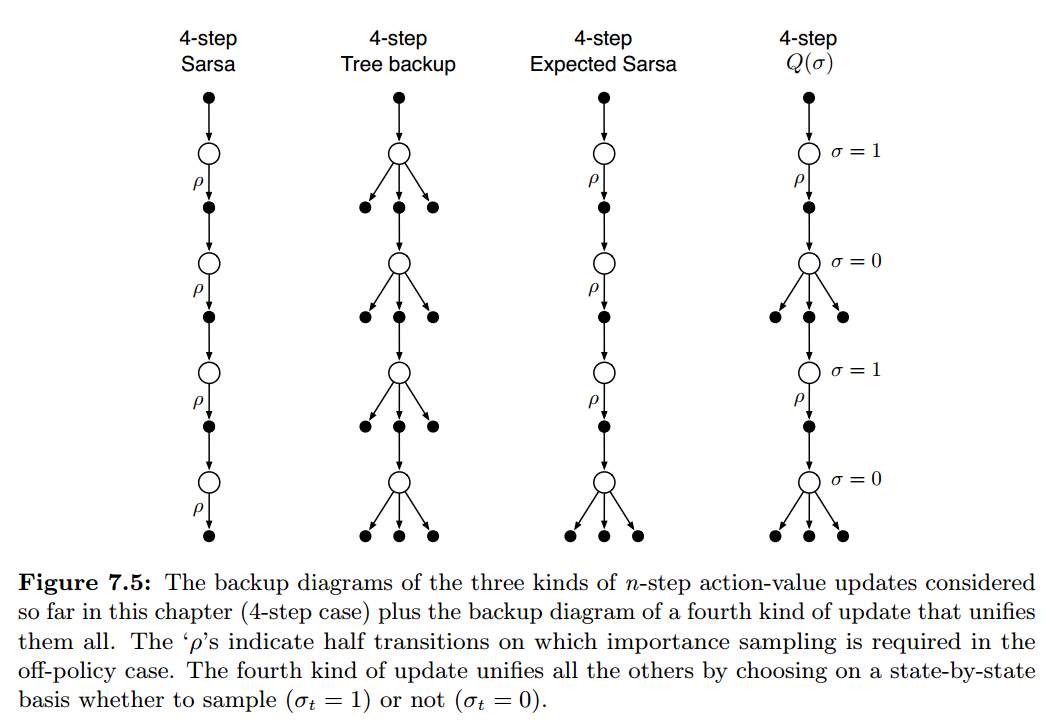
figure_7_5

n-step Sarsa 有所有的转移样本；tree-backup algorithm 则不需要样本，因为它拥有 state-to-action 转移的所有分支；而 n-step Expected Sarsa 拥有最后一步的 state-to-action 带有期望值的完整分支，其它步则拥有转移样本。
将这些算法统一可以得到 $n$-step $Q(\sigma)$.
其思想是算法的每一步均独立决定使用所选动作作为样本，或是使用所有动作的期望。
如果都选前者便是 n-step Sarsa，都选后者就是 tree-backup algorithm，而 n-step Expected Sarsa 则是仅在最后一步选择后者，前面都选择前者。
可以用 $\sigma_t \in [0,1]$ 表示算法在 step t 采样的程度，$\sigma=1$ 表示完全采样，$\sigma=0$ 表示不采样。
随机变量 $\sigma_t$ 可以被设为在 time t 的关于 state、action 或者 state-action pair 的一个函数。

$\begin{align} G_{t:h} & = R_{t+1}+\gamma \sum_{a\neq A_{t+1}}\pi(a|S_{t+1})Q_{h-1}(S_{t+1},a)+\gamma \pi(A_{t+1}|S_{t+1})G_{t+1:h} \\ & =R_{t+1}+\gamma \bar V_{h-1}(S_{t+1})-\gamma \pi(A_{t+1}|S_{t+1})Q_{h-1}(S_{t+1},A_{t+1})+\gamma \pi (A_{t+1}|S_{t+1})G_{t+1:h} \\ & = R_{t+1}+\gamma \pi(A_{t+1}|S_{t+1})\Big(G_{t+1:h}-Q_{h-1}(S_{t+1},A_{t+1})\Big)+\gamma \bar V_{h-1}(S_{t+1}) \end{align}$

它与 7.4 中使用控制变量的 Sarsa 的 n-step return 是相似的，在这两者之间做线性变化：

$G_{t:h}\doteq R_{t+1}+\gamma \Big(\sigma_{t+1}\rho_{t+1}+(1-\sigma_{t+1})\pi(A_{t+1}|S_{t+1})\Big)\Big(G_{t+1:h}-Q_{h-1}(S_{t+1},A_{t+1})\Big)+\gamma \bar V_{h-1}(S_{t+1})$

用它作为 target 结合 $n$-step Sarsa 的更新方法，可以得到 $n$-step $Q(\sigma)$ 的算法：

n-step_Q_sigma

7.7 Summary

本章介绍的时序差分方法是介于 one-step TD 和 MC 之间的。
所有的 n-step 方法均涉及到 n 步延迟更新。且相对于之前的方法，每一步所需要的计算量更大了。
相比于单步方法，n 步方法需要更大的内存，在 12 章，可以看到 multi-step TD 能够用最小的内存灵活地使用 eligibility traces 做增量计算，但是相比于单步方法还是会有额外的计算量。
虽然 n-step 方法比使用 eligibility traces 的方法更加复杂，但它们有一个很大的有点就是计算明了。
使用重要采样率的方法概念简单，但是变数较大，如果行为策略与目标策略差异较大，那就需要新的算法思想来使其更有效率，更实际一些。
使用 tree-backup 的方法在随机目标策略下是从 Q-learning 到 multi-step 很自然的拓展。如果目标策略和行为策略差异较大，那么在 n 比较大时，bootstrapping 可能只能跨越很少的 steps.

ChK