Temporal-difference(TD) learning 是强化学习的核心与亮点。
TD 结合了 蒙特卡洛和动态规划，它可以在没有环境动态的情况下直接利用经验学习，也可以在不等待回报的情况下基于其它估计来进行更新。
同样的，先从 policy evaluation 即 prediction 开始，关注于估计给定策略 $\pi$ 的值函数 $v_\pi$。
对于 control 问题，DP、TD、MC 三种方法都使用了 GPI 的特型，三种方法的主要区别还是在于 prediction 上。

6.1 TD Prediction

TD 和 MC 一样使用经验来解决预测问题。
MC 在某个 visit to s 后会等到 terminal state 得到 return，再使用该 return。
一个适用于 nonstationary environment 的简单的 every-visit MC 法即：

MC 法必须等到 terminal state ，才能得到 $G_t$ 用于更新，而 TD 则只需要等到下一步即可。
简单的 TD 更新如下：

在状态转移后能立即得到 $R_{t+1}$ ，相比于 MC 使用 $G_t$ 更新，这里的 TD 使用的是 $R_t+\gamma V(S_{t+1})$ ，这被称作 $TD(0)$ 或 one-step TD ，另有更广的 $TD(\lambda)$ 或 n-step TD 。
$TD(0)$ 的完整过程如下：

因为 $TD(0)$ 的更新基于已存在的一个估计值，所以称它为 bootstrpping 方法，与 DP 是一样的。
在 DP 中，我们讲到：

简单来讲，MC 用了上式中第一行作为 target ，而 DP 用的是第三行作为 target。
当然，MC 中的 $v$ 是个估计值，因为在 MC 中右边的期望是未知的，MC 使用了多次采样回报的均值来代替它。
在 DP 中的 $v$ 也是个估计值，但并不是因为右边的期望未知了，而是因为它使用了下一个状态的 $v$ ，而这对当前的策略而言是个未知量，所以它使用了当前的估计量。
而在 TD 中，target 是估计值包括了以上两个原因，它既用了采样均值代替期望，又用了下一个状态的估计值。其实，TD 结合了 MC 的采样和 DP 的 bootstrpping.
TD error：$\delta_t\doteq R_{t+1}+\gamma V(S_{t+1})-V(S_t).$ 在强化学习中会以各种形式出现。
TD error 是基于当前时刻所做的估计，因为其依赖于下一个状态与下一个奖励，而这些只能在下一步获得。
也就是说，$\delta_t$ 是一个 $V(S_t)$ 的误差，却只能在时刻 $t+1$ 得到。
另外要注意的是，如果数组 $V$ 在一个 episode 中没有发生变化，那么 MC error 可以写作 TD errors 的和：

如果 $V$ 在 episode 期间有更新，那么该式并不准确，但是只要 step size 足够小，它大致上是成立的。
该式的产生在 TD 算法理论中是很重要的。

Example 6.1：Driving Home

开车回家的例子：每当离开办公室开车回家时，会根据当前时间、今天周几、天气如何以及其它相关信息来预测需要多久到家。
比如说今天是周五，离开办公室时是 6 点整，此时估计需要 30 分钟即 6:30 到家；而当 6:05 走到车旁边时却发现天上下雨了，你认为雨天回家会多花一些时间，那么此时重新估计需要 35 分钟到家，即 6:40 到家；15 分钟后顺利完成高速路部份，于是把估计到家时间改为 6:35；而此时，前方出现了一辆大货车，且路面太窄无法超车，只能慢慢跟车，当到达房子所在街道时已经是 6:40 了，三分钟后最终到家。
这一系列事件与预测总结如下：

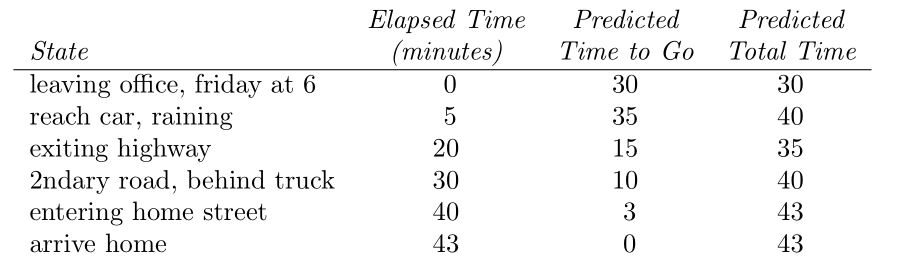
该例中，reward 为每段旅程中消耗的时间(如果是控制问题，可以取负值来最小化)，不使用折扣($\gamma=1$)，即每个状态的回报值为从该状态出发所用的时间，而每个状态的值 value 则为期望时间。
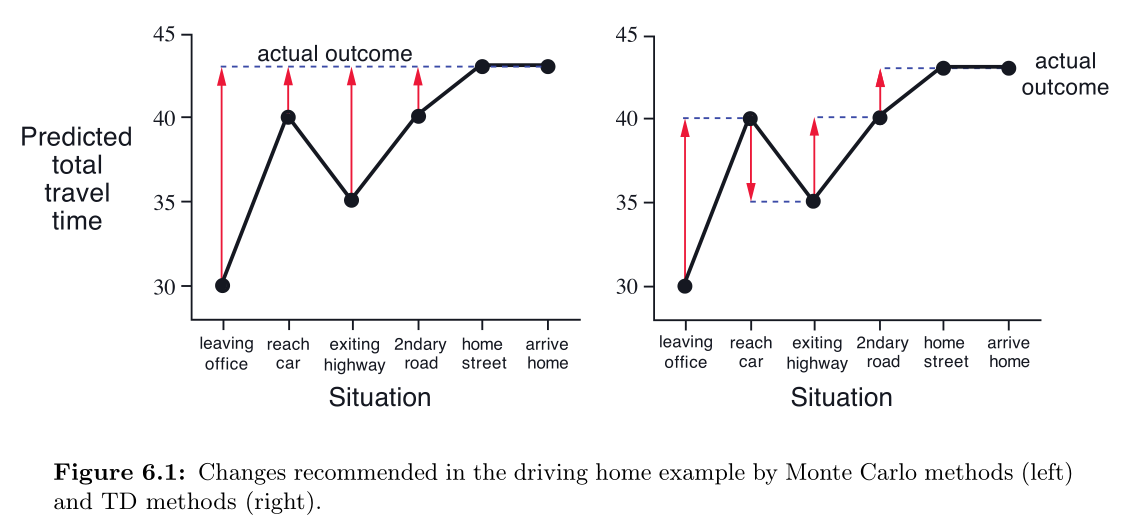
观察 MC 的一个简单方法，如下图左，画出了预测从办公室到家里的总时间。红色箭头表示预测值与实际值的误差。
这里的关键在于是否有必要等到最终回报到达之后再更新值估计，在该例中，刚出办公室的估计是 30 分钟，而假如在路上被卡车堵住只能慢行的时候，最终需要 50 分钟，而此时已经很明确地知道了之前做出的 30 分钟估计是不切实际的估计，这时是否有必要等到最终到家了才来改变估计值。
按照 MC 的方法，是需要等到最终到家，得到真正的回报后才会去更新出门时的估计值的，而如果是 TD 的方法，则在被卡车堵住时便更新了估计值。
在 TD 中，每次变化造成的预测误差都会为最后的预测贡献一部分效果，这就是预测中的 temporal differences.

6.2 Advantages of TD Prediction Methods

TD 相对于 MC 和 DP 的优势在上一节已经有所提及：
TD 相对于 DP ，有一个明显的优势就是其不需要一个环境动态。
而相对于 MC，明显的优势是它可以自然地在线学习，逐步提升。MC 必须等到 terminal state 后才能得到回报用以更新，而 TD 则每一步都能进行更新。这一点是我们选择 TD 最关键的原因，有的应用的 episode 非常长，如果等到 terminal 的话延迟奖励的获取太慢。而有的应用是 continuing task ，根本没有 episode.
并且，有些 MC 方法会忽略或者折扣掉回报，这大大降低了学习速度。
因为 TD 不会管后续动作的选择，而是在每次状态转移后都进行学习，因此 TD 一般不会有这些问题。

TD 虽然很方便，但是需要证明其能够保证收敛。
对于任意给定策略 $\pi$，$TD(0)$ 已经被证明能收敛到 $v_\pi$. 对于足够小的 $\alpha$，如果它根据随机逼近条件来减小，那么其收敛的概率为 1.

TD 和 MC 都能逐渐收敛到准确的 prediction ，但是它们谁收敛得更快，这是一个悬而未决的问题，甚至没有很好的办法来公式化这个问题。
但是在实际应用中，人们感觉在随机任务中， TD 总是会比 constant-$\alpha$ MC 更快收敛。

Example 6.2 Random Walk

针对下以下马尔科夫奖励过程，使用 $TD(0)$ 和 constant-$\alpha$ MC 来对比两者的预测能力：

Markov reward process (MRP)：是没有动作的马尔科夫决策过程，由于它不需要代理所在环境的动态模型，所以可以很好地关注于预测问题。
该例中，所有的 episode 均从状态 C 开始，以等概率向左或向右移动，移动到最右端时结束 episode，并获得奖励 +1，其余情况的奖励均为 0.
因为不使用折扣，所以每个状态的真实值是：从该状态开始，终结于最右节点的概率。
于是，每个状态的真实值如下：从 A 到 E 分别是 $\frac{1}{6},\frac{2}{6},\frac{3}{6},\frac{4}{6},\frac{5}{6}.$

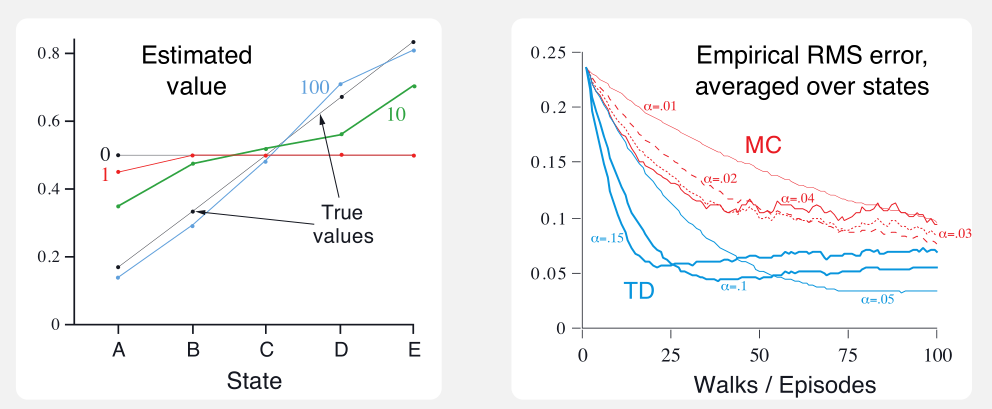
上图左边显示了使用 $TD(0)$ 单次运行不同个数的 episodes 所学得的 values；在 100 个 episodes 后 估计值已经十分接近于真实值了，而根据最后 episodes 的结果，估计值会存在一定的波动。
右图则是不同 $\alpha$ 下两种方法的学习曲线；性能衡量指标是均方根误差(root mean-squared error—RMS)，五种状态经过 100 轮实验后取均值。
每个试验中所有状态的初始估计值均为 0.5.
该例中，TD 始终优于 MC.

6.3 Optimality of $TD(0)$

假设经验是有限的，比如 10 episodes 或 100 episodes，这种情况下，一个简单的办法就是重复利用这段经验，直到方法收敛到某个答案。
给出一个近似值函数 $V$ ,在每次 nonterminal state 的访问中，增量都会被计算，然而值函数却只变化了一次，使用所有增量的和。
然后所有可用经验被再次处理，用于新的值函数，来产生一组全新的增量，这样直到值函数收敛。
将这种方式称作 batch updating ，因为更新仅发生在处理完一组训练数据后。

在这种方式下，只要 $\alpha$ 足够小，$TD(0)$ 会确定性地收敛到一个与 step-size $\alpha$ 无关的结果。
而 constant-$\alpha$ 在同样条件下，也会确定性地收敛，但它们是不同的结果。
理解这两种不同的结果有助于理解两种方法的差异，在一般的更新方法中并不完全是沿着各自 batch answer 的路移动的，但可以说每一步都是朝着这个方向前进的。

Example 6.3 Random walk under batch updating

将 batch-updating 应用在 $TD(0)$ 和 constant-$\alpha$ MC ：每一个新的 episode 后，将所有的 episodes 作为一个 batch.
其余条件与 example 6.2 相同，得到的结果如下图，能看得出来，TD 依然会优于 MC.

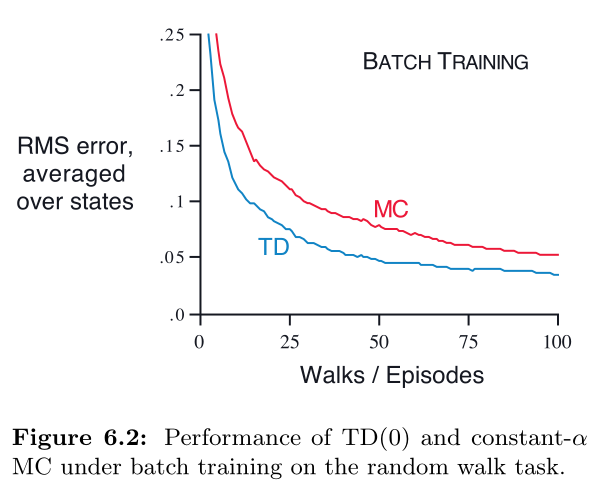
在 batch 训练中，contant-$\alpha$ MC 在访问过 s 后使用了实际回报来更新达到收敛；这从最小化 RMS 的角度来看是最优估计了。
但是 TD 会比 MC 表现更好，是因为 MC 仅在有限路径上是最优的，而 TD 则是在与预测回报相关更大的路径上是最优的。

Example 6.4 You are the Predictor

假设一个预测者观察到一个未知马尔科夫奖励过程的一些 episodes 如下：
A,0,B,0 ; B,1 ; B,1 ; B,1 ; B,1 ; B,1 ; B,1 ; B,0
也就是说，第一个 episode 开始于 A，转移到 B 并获得奖励 0，然后从 B 到终结并获得奖励 0；
其余 7 个 episodes 均开始于 B 并立刻终结，其中 6 个得到奖励 1，剩下 1 个得到奖励 0.
这种情况下，我们可以认为状态 B 的估计值 $V(B)=\frac{3}{4}$ ，但是 A 的估计值有两种情况：
一是按照 batch $TD(0)$ 的方式，A 会以百分百概率转移到 B 且奖励为 0，因此 $V(A)=0+V(B)=\frac{3}{4}$.
二是按照 MC 的方式，我们仅拥有 A 的一个样本，该样本的最终回报为 0， 因此 $V(A)=0$. 而这也的确使得训练集中的 RMS 最小(本例中误差为 0)。
但是我们所希望得到的答案还是第一种，虽然在训练集中第二种的误差是更小的，但是我们有理由相信，在未来可期的数据中，TD 给出的答案才是我们所想要的。

batch MC 找到的估计在训练样本中能达到最小化均方差的效果，而 batch $TD(0)$ 找到的估计能最大可能地得到马尔科夫决策过程的模型。
这个 maximun-likelihood estimate 的参数能够以高概率生成一组非常优质的数据。
在本例中，这个 maximun-likelihood estimate 可以从已观察到的 episode 中看出来：从状态 i 到状态 j 的转移概率的估计值就是已观察到的样本比例数，而对应的期望奖励就是已观察到的奖励均值。
给出了这个模型后，如果模型是准确的，那么就可以计算出准确的值函数估计了；这称作确定性等价估计(certainty-equivalence estimate) ，这相当于假设了潜在过程的估计在某种程度上是已知的，而不是近似的。
一般来说，batch $TD(0)$ 会收敛于 certainty-equivalence estimate.

这解释了为什么 TD 比 MC 收敛得快。
使用 batch 后，$TD(0)$ 比 MC 块是因为它计算了真实的 certainty-equivalence estimate.
而这也可能解释了 nonbatch 下，$TD(0)$ 的速度优势的原因。
尽管 nonbatch 方法不能获得 certainty-equivalence estimate 或 minimum squared-error estimates 的效果，但它可以大致看做是在朝它们过渡的一种方法。
Nonbatch $TD(0)$ 会快于 constant-$\alpha$ MC 的原因可能就在于它正在往更好的估计过渡中。
目前没有更加明确的说法解释 online TD 和 MC 的效率关系了。

最后，虽然 certainty-equivalence estimate 在某种意义上是最优解法，但是它并不适合直接计算。
如果 $n=|\mathcal S|$ 表示状态数，那么仅是建立过程的 maximum-likelihood estimate 就需要 $O(n^2)$ 的内存，而以传统方法计算对应的值函数需要 $O(n^3)$ 步。
而 TD 重复利用样本训练集能够仅在 $O(n)$ 内存下近似得到相同的解。
对于状态空间较大的情况，TD 可能是估计 certainty-equivalence estimate 的最好办法了。

6.4 Sarsa：On-policy TD Control

MC 中需要平衡 exploration 和 exploitation，而解决方式也分为了 on-policy 和 off-policy.
这一节将讨论 on-policy TD control method.
首先要学得一个 动作-值函数 而非 状态-值函数。特别的，对于 on-policy ，必须估计 $q_\pi(s,a)$，这跟预测 $v_\pi$ 的方法是一样的。
回顾一个 episode，其中包含了一系列的 状态 与 状态-动作 的转换：

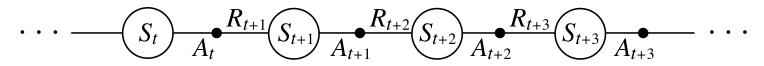
state-action 的转换与值函数的学习，与单纯的 state 情况没有什么不同；它们都是包含奖励过程的马尔科夫链，保证收敛下的更新规则是一样的：

该规则用上了转移过程中的五元组 $(S_t,A_t,R_{t+1},S_{t+1},A_{t+1})$ ，这种算法叫做 Sarsa.
根据 Sarsa 构造 on-policy control 算法是很简单的；与其它 on-policy 方法相同，先根据 behavior policy $\pi$ 估计其值 $q_\pi$ ，同时依据 $q_\pi$ 调整策略 $\pi$ 使其更加贪婪，也就优于旧策略。
Sarsa 的收敛表现取决于策略对 Q 的依赖程度。

6.5 Q-learning: Off-policy TD Control

早期强化学习的一个重大突破就是 off-policy TD control algorithm 的提出，即 Q-learning(Watkins,1989)：

它学习的 action-value function Q 是直接逼近最优值函数 $q_\ast$ 的，而不是当前遵循的策略的值函数 $q_\pi$.
这大幅度简化了算法的分析，并且能够更早地验证收敛。
策略依然决定了哪些 state-action pairs 被访问和更新；但是这只是为了使得所有的组合都被访问与更新过，以此来保证收敛。
而这仅仅是任何想要取得最优行为的方法所必须遵守的一个最低要求。
在该假设以及一些常见的对 step-size parameters 的随机逼近约束下，Q 能够以概率 1 收敛到 $q_\ast$

Example 6.6: Cliff Walking

如下的 gridworld 是一个标准的 undiscounted，episodic task，动作为上下左右的移动，所以转移都会带来奖励 -1，而如果走进了 “The Cliff” 区域，奖励值为 -100，并且转移到初始状态，即回到 S；终止状态为 G.

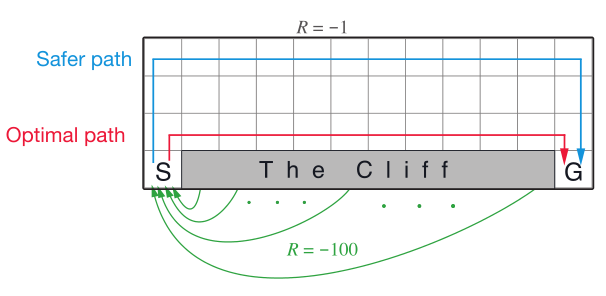
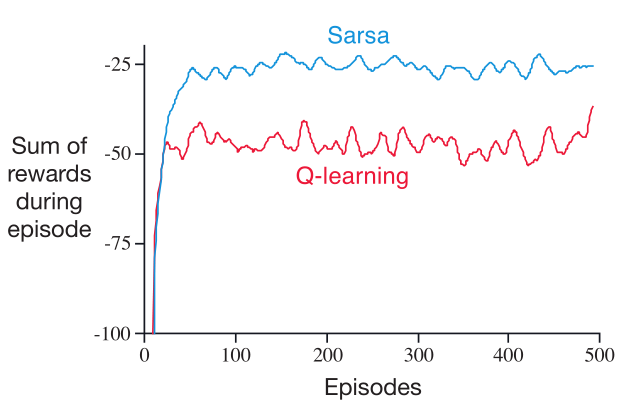
上图则显示了使用 $\epsilon=1$ 的 Sarsa 和 Q-learning 的性能；在初始的转移后，Q-learning 学到了最优策略的值，沿着 cliff 区域的边缘走，但是这个策略由于 $\epsilon$-greedy 有时会走进 cliff 区域。
而 Sarsa 则学到了一条相对远却更加安全的路线，沿着网格的顶部走。
尽管 Q-learning 学到了最优策略，但是其 online 的表现却不如 Sarsa 学到的迂回策略；当然，如果 $\epsilon$ 逐渐减小，那么两个方法最终都会收敛到最优策略的。

6.6 Expected Sarsa

与 Q-learning 的区别在于将最大值 $\max_aQ(S_{t+1},a)$ 替换成了期望值 $\mathbb E_\pi\big[Q(S_{t+1},A_{t+1})\mid S_{t+1}\big]$ ，公式为：

它的模式与 Q-learning 是一样的。给定下一个状态 $S_{t+1}$，该算法能确定的走上期望中的 Sarsa 所前进的方向。
Expected Sarsa 在计算上比 Sarsa 复杂一些，但是消除了由于随机选择 $A_{t+1}$ 所造成的不确定性。 在相同数量的经验下，它的表现会略优于 Sarsa.
下图显示了在 cliff-walking 中三种方法的大致效果：

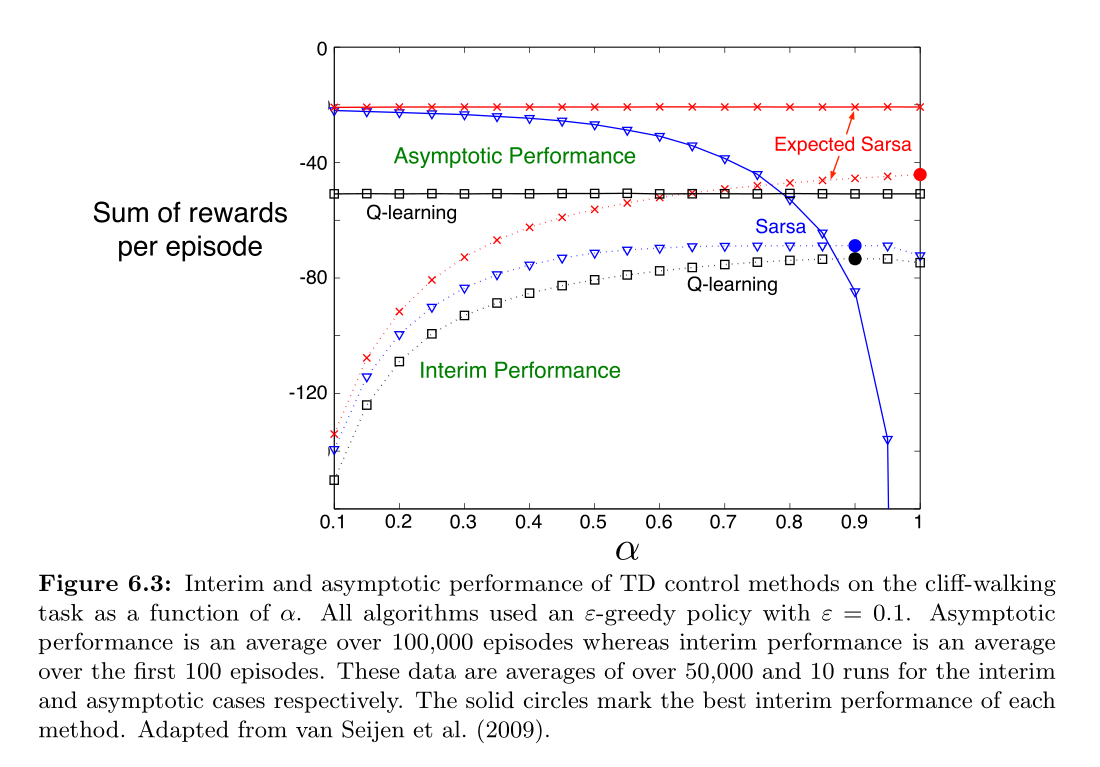
Expected Sarsa 表现出了巨大的优越性，在不同的 $\alpha$ 范围内，expected Sarsa 均表现出优于 Sarsa 的性能。
在 cliff walking 中，所有的状态转移都是确定的，而所有的随机性均来自于策略。
在这种情况下，Expected Sarsa 可以将 $\alpha$ 设为 1，而不会导致性能的降低；而 Sarsa 只能长期保持一个小的 $\alpha$ 才能拥有足够优越的性能，短期的表现很差。
在许多情况下，Expected Sarsa 都能保持类似该例中的相对于 Sarsa 的优势。

在该例中，Expected Sarsa 用的是 on-policy，但是在许多情况下，它会使用 off-policy 形式。
比如说，如果 $\pi$ 是一个贪婪策略，而行为策略更具探索性，那么 Expected Sarsa 就是一个 Q-learning 了(因为 $\pi$ 是贪婪的，它只选择值最高的那个动作，那么 $A_{t+1}$ 的期望值就是 greedy-action 的值了)。
在这个层面上，Expected Sarsa 包含了 Q-learning 且完全优于了 Sarsa.
除了需要一点额外的计算消耗外，Expected Sarsa 可以说是全面超越了另外更知名的 TD control algorithms.

6.7 Maximization Bias and Double Learning

以上提到的所有控制算法均涉及到了一个构造目标策略的最大化的问题。
比如 Q-learning 中，目标策略时贪婪的，这就涉及到了最大的 动作值；
而在 Sarsa 中策略经常是 $\epsilon$-greedy ，也涉及到了一个最大化的操作。
在这些算法中，隐含地使用最大估计值作为最大值的估计，这可能带来一些较大的正偏差。
比如一个状态 s 有多个动作的真实值为 0，但估计值是不确定的，分布于 0 的左右；那么最大的真实值是 0，但最大的估计值会是正的，这就是一个正的偏差。被称作 maximization bias.

Example 6.7： Maximization Bias Example

下图提供了一个简单地例子，表明 maximization bias 是如何降低 TD 控制算法的性能的，其中涉及的是一个很小的 MDP.

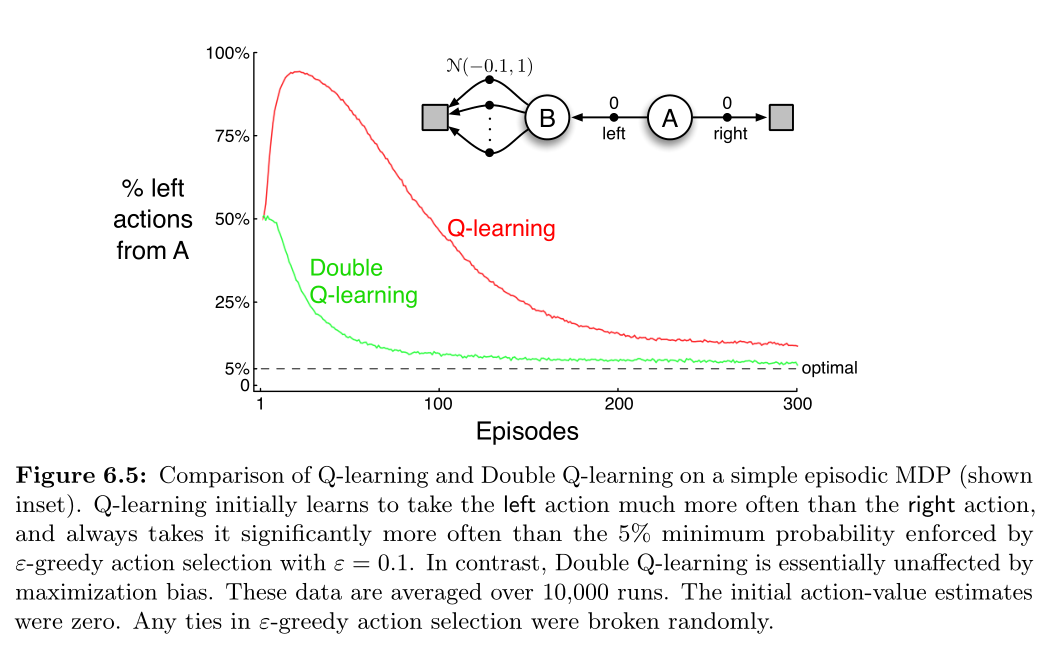
该 MDP 有两个 non-terminal states A and B；episodes 总是从 A 开始，向左或向右移动。
右移会立刻到达 terminal state ，奖励为 0；左移会到达 B ，奖励也为 0.
而从 B 开始有多个动作，所有动作都会立刻转移到 terminal state，但是奖励值则取自 标准分布($mean=-0.1, variance=1.0$)
因此，A 向左移动带来的期望回报应该是 -0.1. 所以左移并不是一个明智的选择。
然而，maximization bias 会使得控制方法更偏爱 左移，因为左移有时会带来正的回报值。
上图表现出 Q-learning 一开始的时候会极度偏好左移，即使在逐渐收敛后，也仍然比最优策略要高出 $5\%$ 的几率选择左移。
Q-learning 会出现 maximization bias 是因为在选择动作和估计其值时都是用的同一个 Q.
double learning 使用两个不同的 Q 分别来选择动作和估计期望值；比如用 $Q_1$ 选择动作： $A^\ast=\arg\max_aQ_1(A)$，然后用 $Q_2$ 来估计其值： $Q_2(A^\ast)=Q_2(\arg\max_aQ_1(a))$. 这样估计值就会是无偏的了：$\mathbb E[Q_2(A^\ast)]=q(A^\ast).$
这会使得内存消耗翻倍，但是计算步数是不变的。
double learning 扩展了完整 MDPs 的算法。比如说，将 double learning 用在 Q-learning 上，就叫 Double Q-learning，随机地选择更新 $Q_1$ 还是 $Q_2$:

如果是更新 $Q_2$，只要将两者互换即可。它们完全是被对称对待的。
行为策略可以使用两个 动作-值函数。比如将两个值函数的均值作为更新依据。
下面是完整的 Double Q-learning 的算法：

6.8 Games, Afterstates, and Other Special Cases

我们之前学到的多数方法涉及的是 action-value function.
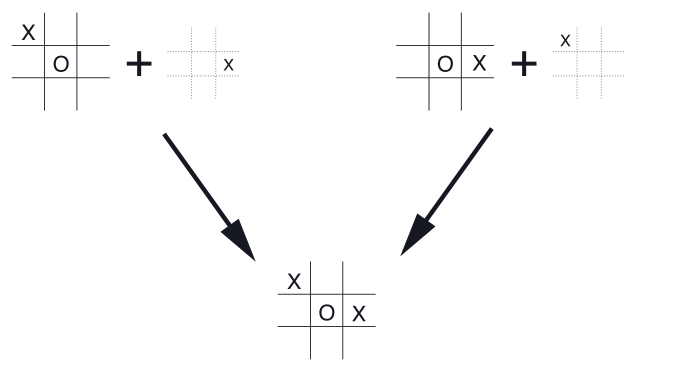
而在第一章中的 tic-tac-toe 游戏中，它涉及的不像是 action-value function，然而也不是 state-value function.
传统的 state-value 估计的状态是在 agent 选择动作之前；而在 tic-tac-toe 中，所估计的是在 agent 落子后的棋盘局势，这是 action 发生之后的状态值；而落子后下一个 state 是由对手来决定的。
这叫做 afterstate，对应的值函数叫 afterstate value functions.
afterstates 适用的情况是：知道环境动态的初始部份信息，但是不知道完整的环境动态。
在三连棋游戏中就是知道了我落子后棋盘会如何变化，但是不知道对方会如何应对，那么自然就不知道后续的变化了。
在这种情况下，是可以利用这个已知的立即变化来优化得到一个更加有效率的学习方法的。
一个传统的 action-value function 是将状态与动作组合一起来估计其值的，而在 afterstate 中，我们可以看到不同的状态动作组合可能会导致完全相同的下一个状态，而相同的状态拥有的是相同的值：