动态规划(dynamic programming, DP)指的是一类算法，该类算法用于在已知环境的完全模型的情况(比如 MDP )下，计算出最优策略
DP 在 RL 中应用有限，因为其要求有环境的完整模型，以及其计算量消耗巨大，但它依然是很重要的理论基础，有助于理解后续的方法
实际上，后面的方法可以看做是试图用更少的计算量，无需完全环境模型的方法，达到 DP 的效果

首先，假设环境是 finite MDP ，即状态、动作、奖励的空间是有限的
对于连续空间的问题，可以量化其三个空间，然后使用 finite-state DP

DP 的关键在于利用 值函数 来组织构造对优等策略的搜索
我们已知，如果有了满足贝尔曼最优方程的 $v_\ast$ 或 $q_\ast$ ，就能轻易地得到最优策略
DP 会把贝尔曼方程转化为逼近所求 值函数 的更新规则

4.1 Policy Evaluation (Prediction)

policy evaluation(prediction)：如何为任意策略 $\pi$ 计算其 state-value function $v_\pi$
上一章我们给出了 $v_\pi$ 定义：

如果环境动态完全已知( $p$ 已知)，那么上式就是 $|\mathcal S|$ 个未知数的 $|\mathcal S|$ 个非线性方程组
原则上，它的解是简单易算的
针对我们的目标，迭代解法更为合适
考虑一组估计值 $v_0,v_1,v_2,\dots,$ 每一个都是从 $\mathcal S_+$ 到 $\mathbb R$ 的映射，初始估计值 $v_0$ 随机选取，后续的估计值就能用上式作为更新规则来获得

在此更新规则中，$v_k=v_\pi$ 是固定的，而 $v_\pi$ 的贝尔曼方程保证了该例中的相等性
实际上，在相同条件下，序列 ${v_k}$ 在 $k\rightarrow \infty$ 时会收敛于 $v_\pi$
该算法称为迭代策略估计(iterative policy evaluation)

算法对每个状态 $s$ 执行相同的操作，来从 $v_k$ 得到 $v_{k+1}$
它使用旧的 values 的后续状态，和当前策略的所有可能的单步转移所得的期望立即奖励，来得到一个新的 value ，并以新的替换旧的
这种操作称为 expected update
每一次的迭代都会把所有的状态的值都更新一遍，来得到一个新的逼近值函数 $v_{k+1}$
DP 的更新称作期望更新，是因为它是基于所有可能的后一状态的值的期望，而不是仅基于后一状态的一个采样

编程实现以上的迭代策略估计时，会用到两个数组，一个用于存放 old values $v_k(s)$ ，另一个存放 new values $v_{k+1}(s)$
使用两个数组，能在 old values 不变的情况下，更新 new values
如果只用一个数组，在原地将 old values 更新为 new values，那么有些部分就会用 new values 代替 old values 作为更新依据，这也能让算法收敛于 $v_\pi$; 事实上，这样做的收敛速度会快于使用两个数组，因为它一得到最新数据就把它用来更新
我们把这更新看做在状态空间中的 sweep ，对于原地更新算法，更新时候的状态顺序会对收敛速度起到很大的影响
我们在考虑 DP 算法时通常会使用 原地更新

一个完整的迭代策略估计的原地更新算法如下
理论上讲，算法只会在无穷远处收敛，然后停止迭代
我们在实践中，会在每次 sweep 后检查 $\max_{s\in \mathcal S}|v_{k+1}(s)-v_k(s)|$ ，当它足够小时，就停止迭代

Example 4.1

一个 $4\times 4$ gridworld：

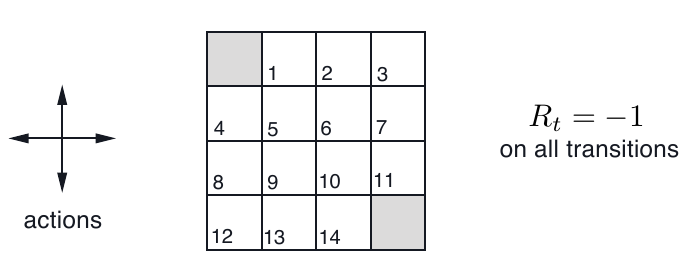
图中，阴影的两块位置为 terminal state (虽然有两块，但只表示一个状态)
所有的状态转移所得到的 reward 均为 -1
也就是说，无论 agent 怎么行动，都会得到 -1 的 reward ，直到它到达 terminal state
不过要注意，在格子的边缘，如果走向离开格子世界的地方，就会保持在原地不动，同时得到 -1 的 reward
比如， $p(7,-1\mid 7,right)=1$， 表示在格子 7 向右走，下一个格子是 7 ，得到 reward -1 的概率为 1
所以 agent 的学习目标就是尽快到达 terminal state
下图是该例的迭代策略估计的更新过程：

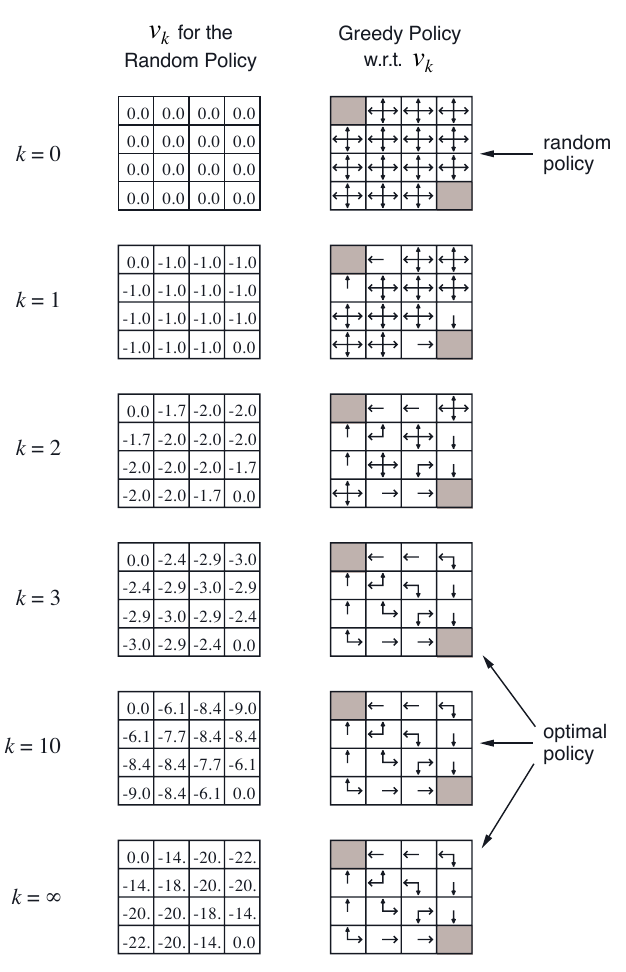
这里，$k=3$ 时，位置 6,9 之所以不走向 2,7,8,13 的原因是，走向它们会使得 agent 有更多的可能进行 “出格” 的行动，而走出格子世界会使得状态不变而奖励 -1 ，这相当于在做负功
更新过程中，始终用的是等概率策略，右边显示的 greedy policy 并不是在更新过程中使用的 policy

Exercise

4.1：

4.2：

待做

4.3：

4.2 Policy Improvement

计算 值函数 是为了找到更好的 policy
假设我们对一个随机的确定性策略 $\pi$ 确定了其 值函数
在某些状态 $s$ 时，我们会想知道是否应该去选择由策略所得到的那个 action，转而选择一个 action $a\neq \pi(s)$
我们现在知道，在 $s$ 使用当前策略有多好—$v_\pi(s)$ ，但改变策略会不会得到更好的结果呢？
我们可以试着去选择这个 $a\neq \pi(s)$

关键在于这个值与 $v_\pi(s)$ 的大小关系
如果 $q_\pi(s,a) > v_\pi(s)$ ，那么我们不只希望这一次选择这个 action ，还希望在未来遇到这个 $s$ 的时候，依然会选择这个 action a

policy improvement theorem.： $q_\pi(s,\pi’(s)) > v_\pi(s).\quad \text{for all } s\in \mathcal S$
表明策略 $\pi’$ 优于策略 $\pi$： $v_{\pi’}(s) > v_\pi(s).\quad \text{for all } s\in \mathcal S$

照下式更新策略，即可使得新的策略不差于原始的策略，这就是 policy improvement：

当新的策略与旧的策略相同时，就说明其收敛；且根据贝尔曼最优方程，其必然是最优策略

policy improvement 会给我们一个优于原策略的新策略，除非原策略已经是最优策略
在更新过程中，如果旧的贪婪策略中有多个 greedy action ，那么在新的贪婪策略中，可以为他们分配相同的概率，而不是随机选一个

4.3 Policy Iteration

在用 $v_\pi$ 优化原策略得到新策略 $\pi’$ 后，就可以用新策略来计算新的值函数 $v_{\pi’}$ ,然后，继续优化：

其中 $\stackrel{E}{\longrightarrow}$ 表示 policy evaluation，而 $\stackrel{I}{\longrightarrow}$ 表示 policy improvement
finite MDP 有 finite policies，从而该过程在 有限次迭代 后会收敛于 最优策略 和 最优值函数
以上称为 policy iteration，其完整算法如下
起始的策略对迭代的收敛速度有较大的影响

策略迭代经常会非常快地收敛

Example 4.2： Jack’s Car Rental

一个出租车公司，有两个出租点，每租出一辆车收获 10 ，如果出租点没有车，交易失败，可以在两个出租点之间调整车辆，每移动一辆车耗费 2
假设 租车需求 和 还车数 都是随机变量(泊松分布)， 即取值为 n 的概率是 $\frac{\lambda^n}{n!}e^{-\lambda}$ ，此处 $\lambda$ 是期望值。 设两个出租点的 出租需求 的期望 $\lambda$ 分别为 3 和 4；还车数 的期望 $\lambda$ 分别为 3 和 2 ，假设每个点的车辆数目不超过20，超过的部分会消失； 每次移动车辆最多 5 辆
将该问题视作 continuing finite MDP， time step 为每天，$\gamma=0.9$ ；state 为每天结束时两个点的车辆数，action 为每晚移动车辆的数目
下图显示了 $\pi$ 的变化， 是一个矩阵，矩阵各区域的取值显示在图上

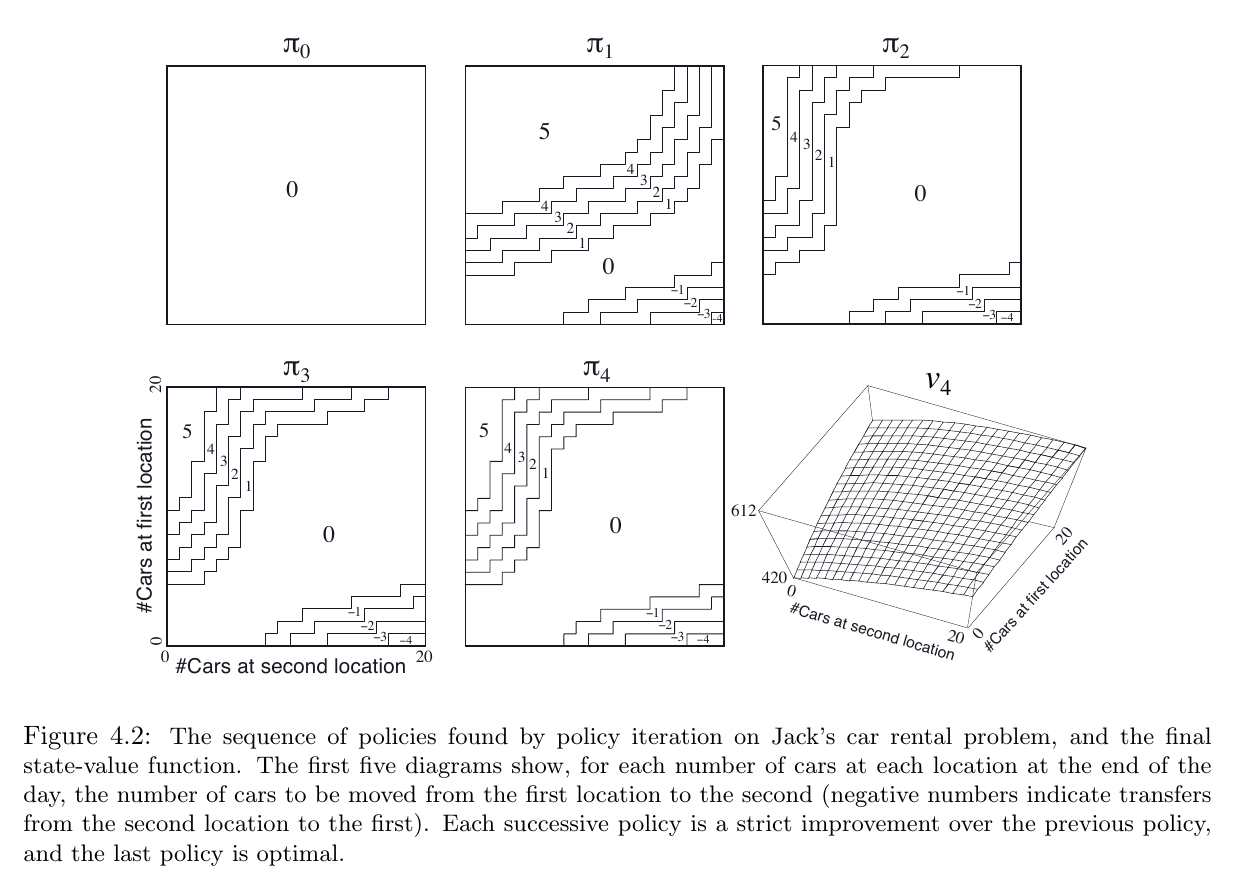
Exercise

4.4：
限制迭代轮次？？

4.5-4.7：

先跳过

4.4 Value Iteration

policy iteraion 的缺点之一：每轮迭代都有 policy evaluation ，它本身就是一个较长的迭代过程，需要多次 sweep 计算
如果 policy evaluation 是迭代完成的，那么只有在极限处才会 完全收敛至 $v_\pi$

可以截短 policy evaluation ：
在保证 policy iteration 能够收敛的情况下，有多种方法截短 policy evaluation
一个重要且特殊的算法 value iteration：在 evaluation 进行了一次 sweep (每个 state 都更新过一遍) 后立刻停止
policy improvement 和 截短的 policy evaluation 的单步结合可以写作：

如何理解：1.贝尔曼最优方程 的更新规则表达；2.树状图 (policy evaluation && value iteation)

迭代终止：理论上会在 有限次数 迭代后 收敛至 $v_\ast$ ；实践中，与 policy evaluation 一样，在某次 sweep 后，如果 value function 的变化小于某个预设值，即可停止；完整算法如下：

value iteration 在一个 sweep 中有效结合了： policy evaluation 和 policy improvement
很多时候，在每个 policy improvement sweep 中插入多个 policy evaluation sweeps 能够带来更快的收敛
一般来说，整类 截短 policy iteration 方法可以看做是 考虑不同序列的 sweeps 组合，哪些用 policy evaluation updates，哪些用 value iteration updates
这两种 updates 之间的差别在于公式中的 $\max_a$ ；这意味着，我们是在 某些 policy evaluation sweeps 中加入了这个 $\max_a$
在 discounted finite MDPs 中，这些算法总是能收敛到一个 最优策略

Example 4.3： Gambler’s Problem

一个赌徒玩猜硬币：人头向上则赌注翻倍，人头向下则赌注没收；本钱达到 100 或 0 则游戏结束；赌徒所做的抉择是，每次丢硬币前押多少本钱
该问题可以形式化为一个 无折扣的、周期式的、有限马尔科夫决策过程
state： 赌徒的本钱数量： $s\in\lbrace1,2,\dots , 99\rbrace$
actions：每次赌注数目： $a\in \lbrace 0,1,\dots,\min(s,100-s)\rbrace$
reward： 除了获胜(本钱达到 100)时为 +1 外，其余的状态转移均为 0
state-value function： 当前 state 的获胜概率
policy： 本钱 $\rightarrow$ 赌注 的映射
设 $p_h$ 为硬币人头向上的概率，如果 $p_h$ 已知，那么整个问题就是已知的，就能够解决了，比如用 value iteration
下图显示了 value function 随 value iteration 的连续 sweep 的变化情况，以及最后找到的 policy ，其 $p_h=0,.4$
该策略最优，但不是唯一的；实际上，有一组最优策略，它们关于与 最优值函数 的 argmax action 的选择方式有关联

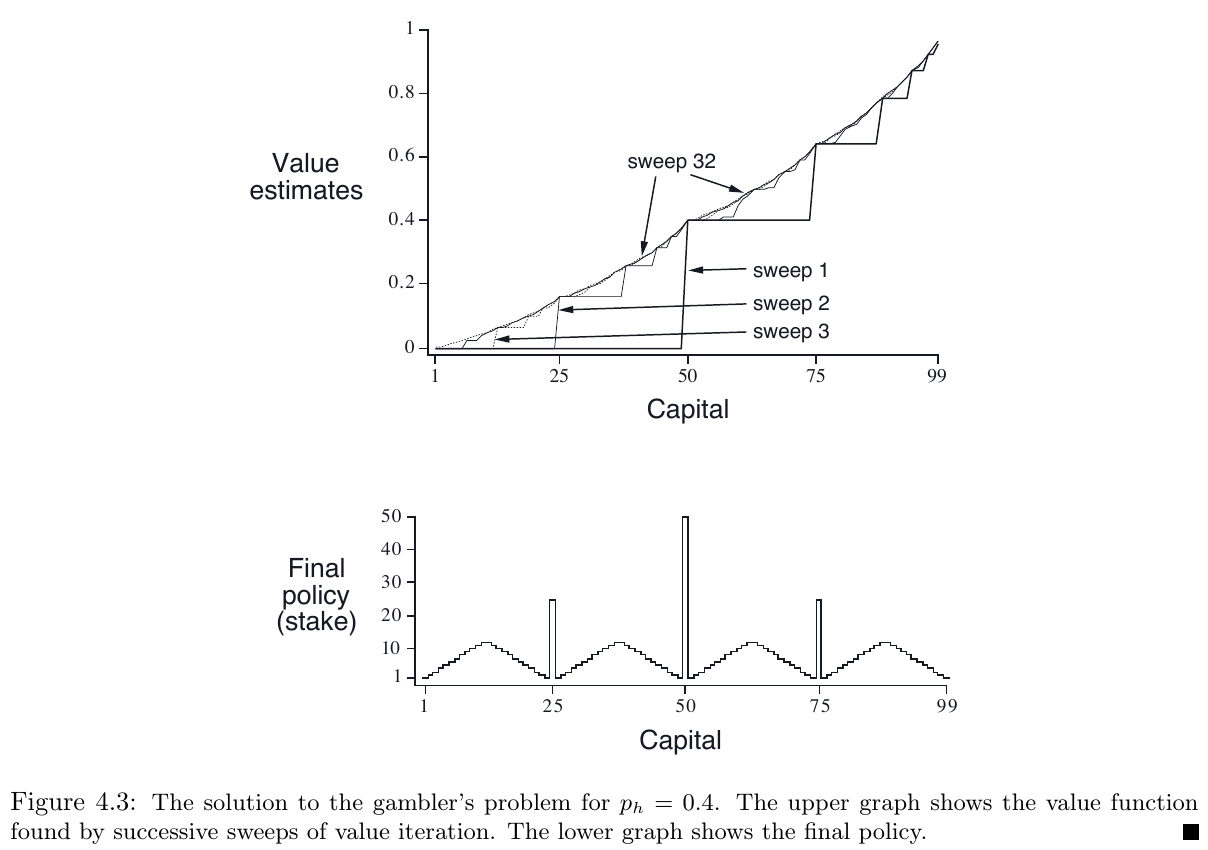
Exercise

4.9-4.10：

先跳过 

4.5 Asynchronous Dynamic Programming

DP 需要遍历 MDP 的整个状态集，如果状态集很大的话，一次 sweep 就难如登天了
backgammon 就有超过 $10^{20}$ 个状态，即便我们能在一秒内 计算 100万 状态的 value iteration ，一个完整的 sweep 也将耗费超过一千年的时间
Asynchronous DP 是一种 原地 迭代的 DP 算法，不对状态集进行系统的 sweeps
异步DP 使用任意可用状态的 value，以任意顺序 更新 状态的 values
可能有些状态被更新了许多次，而某些状态只被更新一次
为了能够收敛，异步DP 要持续更新所有的状态，并不会在某些情况下忽略任意状态的计算
异步DP 在选择更新的状态上有很高的灵活性

举个例子：
asynchronous value iteration：在每个 step $k$ ，只更新一个状态 $s_k$
如果 $0 \leq \gamma < 1$ ，保证在无穷的时间序列 ${s_k}$ 中出现过所有的状态下，能够让算法逐渐趋近 $v_\ast$
在一些 undiscounted episodic case 中，有一些更新顺序会导致算法无法收敛，但这很容易避免
类似地，可以混合策略评估和值迭代更新以产生一种异步截断的策略迭代
虽然这个和其他更不寻常的DP算法的细节超出了本书的范围，但很明显，一些不同的更新形成了可以在各种无扫描DP算法中灵活使用的构建块

避免 sweeps 比不意味着能够减少计算量
它只能让算法在优化 policy 之前，无需锁定在任何 无用冗长的 sweep 上
利用选择更新状态的灵活性，可以加快算法的更新速率
可以通过调整更新顺序，使得状态转移时的信息传递更有效率
有些状态可能并不需要很多的更新，有时我们会完全跳过某些状态的更新，因为它们与最优动作无关，在 Chapter 8 中讨论

异步算法使得在实时交互中混入计算过程变得容易
可以在 agent 实际经历 MDP 的同时运行迭代 DP 算法
agent 的经历用于决定 DP 算法更新哪些状态
同时，DP 算法的最新 value 和 policy 可以指导 agent 的决策
比如，可以在 agent 访问到时 才提供状态的更新；这使得 DP 算法关注更新的状态与 agent 的行为密切相关
这种 focusing 是 RL 中一个被不断讨论的主题

4.6 Generalized Policy Iteration

policy iteration 同时包含了两个交互过程：

1. policy evaluation： 使 value function 对应当前的 policy
2. policy improvement： 使 policy 为当前 value function 的 greedy 选择

在 policy iteration 中，它们是交替进行的，这不是必要的
在 value iteration 中， 两次 policy improvement 之间只执行一次 policy evaluation
而在 异步 DP 中，两者以更加精细的方式交错，在某些时候仅仅更新了一个状态就转头去进行另一个更新
只要这两个过程持续更新所有的状态，最终结果是一样的，那就是收敛于 最优值函数 和 最优策略

generalized policy iteration (GPI) ：evaluation 与 improvement 的交互，不论两者交错的粒度或其它的细节
几乎所有的 RL 方法都能用 GPI 来描述
它们都有可识别的 policies 和 value functions； evaluation 总是会给出当前 policy 对应的 value function； improvement 总是会利用其 value function 优化当前的 policy
当它们不再变化时，表明达到了最优；即当前的 policy 已经无可优化，且当前的 value fucntion 已经对应了当前的 policy
这就是贝尔曼最优方程所表达的

在 GPI 中，evaluation 和 improvement 可以看做是矛盾双方，在竞争中协调进步
evaluation 要使 value function 对应于当前的 policy
improvement 要使 policy 优于 当前 value function 对应的那个 policy，就会使得 value function 与 policy 再次不对应

总而言之， GPI 的两个过程会把算法带向最优，只要这个最优是存在的

4.7 Efficiency of Dynamic Programming

DP 在较大的问题上不实用，但相比其它解决 MDPs 的方法，DP 的效率很高
DP 找到 最优策略的的时间是关于 状态空间 $n$ 和 动作空间的 $k$ 的多项式
这大大优于直接搜索策略空间 (大小约为 $k^n$ )的那些方法
线性规划也能用于 解决 MDPs，且在某些情况下其收敛性能比 DP 要好，但是它能适应的问题大小比 DP 小得多 (差距大约 100倍)
对于那些最大的问题，只有 DP 是可行的

由于维度灾难(curse of dimensionality)，DP 有时被认为有巨大的应用限制
实际上，这不是 DP 不好用，而是其面临的问题难度太大，DP 已经比暴力搜索、线性规划好得多了

现如今的计算机，已经能用 DP 解决具有 百万状态的 MDPs
policy iteration 和 value iteration 都被广泛应用，不能说哪一个会更好
如果有一个不错的初始 value function 和 policy ，那么它们的收敛速度还是很可观的

对于状态空间较大的问题，常使用 异步DP
用同步方法对每个状态完成一次 sweep 需要的计算和内存太大
在某些问题中，虽然其所需的计算和内存不能满足，但也能解决问题，是因为在通往最优方案的路径中，所涉及的 状态 要比其状态空间小得多

4.8 Summary

学习了解决 finite MDPs 的 DP 算法
policy evaluation 用于计算一个 给定 policy 对应的 value function
policy improvement 用于在 给定 policy 及其对应的 value function 的基础上，计算更优的 policy
两者结合，就有了 policy iteration 和 value iteration 这两个 DP 方法
它们都可用于计算一个完全已知 MDP 的 finite MDPs 的 最优值函数 和 最优策略

经典 DP 方法针对 状态集 做 sweep，对所有的 state 做 期望更新
期望更新 与 贝尔曼方程的联系更紧，它用到了 当前状态的所有可能后续状态 的期望变化情况
当 更新 不再带来变化时，算法收敛，满足贝尔曼方程

GPI 是对 DP 中两个过程之间的交互关系 表达，忽略了交错的细节

bootstrapping：在某些估计值的基础上，更新原有的估计值；用多次抽样来回归母本分布
因为 DP 是需要环境的完全模型的，但这一点很难实现，所以用 bootstrapping 来模拟
下一章将讨论 不需要模型且不用 bootstrapping 的方法
后面的章节将讨论 不需要模型但是使用了 bootstrapping 的方法