区分强化学习与其它机器学习方法的最重要特征：用 评价动作选择的训练信息(用 policy 来选择动作，强化学习会评价所选择的动作的好坏) 来取代 直接给出正确动作的指导信息 (由外部直接给定正确的动作) 。为了明确搜索好的行为，强化学习需要积极地探索。单纯的评价性反馈指出采取的动作有多好，而不是说哪个动作最好或哪个最差；而单纯的指导性反馈恰恰相反，其指出应该采取的正确动作。在这种单纯的形式上，这两种反馈有明显不同，评价性反馈完全依赖于动作的选取，而指导性反馈则完全独立于动作的选取。

这一章在一种简单的环境下(不超过一种situation， 选择 action 时不用考虑 state ，因为 state 是始终不变的常量)学习评价方面的RL，这种无关联环境中，评价性反馈所涉及的前置工作已经完成，避免了完整的RL问题中的许多复杂情况。学习这个例子，能够清楚地了解评价性反馈是如何区别于指导性反馈，以及如何与其相结合。

这章使用的无关联、评价性反馈问题是 k-armed bandit proble 的一种简单版本，用它来引入一系列基本学习方法，并在后续章节中扩展他们以应用于完整的RL问题。在本章的最后，通过讨论 bandit 问题变成 associative ，即 situation 多于一种的情况下的RL问题。

2.1 A k-armed Bandit Problem

所谓 Bandit Problem ，就是指要在一个动作空间中做出选择，然后该选择将会决定获得的奖励的多少，在不停的做选择并得到奖励回馈中不断优化选择策略。

此处的问题中，需要在k个不同选项中重复地做选择，每次选择后会得到一个数值奖励，其出自一个依赖于所做选择的统计概率分布，目标是在经过一段时间(如1000次选择或一段实际的时间)让总奖励的期望最大化。

在该问题中，每个 action 都有一个期望或平均奖励，称为该 action 的 value (这里的 value 与后面的 value function 有所不同，在这个问题中，action 不会影响到后续 states 的变化，因此 action 只对立即奖励有影响，而对长期累计奖励没有影响，而后面讨论到的问题没有这么简单)。将在 time step $t$ 做的选择定为 $A_t$，其对应的奖励值为 $R_t$，对任一 action $a$，定义 $q_\ast (a)$ 为 $a$ 的期望奖励:

由于 $q_\ast (a)$ 不完全可知，定义 estimated value of action 为 $Q_t(a)$，目标是让 $Q_t(a)$ 靠近 $q_\ast (a)$
这里的 $q_\ast (a)$ 的定义是针对 Bandit Problem 的，每次的选择不会影响到后面的情况，因此只要考虑即时 reward

当我们保存下这些 estimates of the action values ，在某些 time step 中，我们能够找到 value 最高的 action ，它们称为 greedy action ，如果我们选择这些action，就叫做 exploiting ；反之，当我们选择那些不是 greedy actions 的 action 时，称作 exploring ，这能优化那些 non-greedy action 的 value ，这主要依赖于后续的未知变化。

在任意确定案例中， explore 和 exploit 哪个好是一件很复杂的事情，其取决于估计的精确值，不确定性及剩余步数。在 bandit problems 和其它相关问题中，能够用特定的数学表达来得到许多精妙的方法来平衡这两者，但是这些方法大都对平稳和先验做了强假设，它们都不能实际应用在完全的RL问题中，当这些理论假设不成立时，这些方法的优化和有限损失的保证均不靠谱。

2.2 Action-value Methods

对 action-value 的估计可以简单地表示为：

分子为在 $t$ 时刻前所有选择 action $a$ 所获得的 rewards 之和，分母为在 $t$ 时刻前选择 action $a$ 的总次数。

$Q_t(a)$ 表示选择一次 action $a$ 所获得的平均 reward 。特别地，当分母为0时，可以定义 $Q_t(a)$ 为0.

当分母趋于无穷时，根据大数定理，$Q_t(a)$ 趋于 $q_\ast (a)$ ，该方法称为 sample-average technique

最简单的 action 选取规则就是选择拥有最高 estimated value 的那个 action ，当有多个 actions 拥有最高 estimated value 时，任意选择其中一个即可，即：

该方法是完全 exploit ，不进行 explore ，一个简单的改进是引入一个概率值 $\epsilon$，来使选取策略以一定概率进行 explore ，即不再选择拥有最高 estimated value 的 action ，而是随机选取 action ，这称为 $\epsilon$-greedy methods 。该方法的优势在于，随着 steps 的增加，每个 action 总会有机会被选中，使得 $Q_t(a)$ 整体上趋于 $q_\ast (a)$

Exercise：

2.1：

• $50\%$

2.2：Bandit example：

• A2、A5肯定是 ε case ，因为在A2以前， action 2 没有被选择过，其Q值为0，而 action 1 的Q值已经非0，当时的 greedy action 应该是 action 1 ，所以 action 2 肯定不是 greedy action ，A5同理；A1、A3有可能是 ε case ，在 time step 3 ， greedy action 应该是 action 1 以及 action 2 ，按照对 greedy action 的选取策略，如果是随机选中到了 action 1 ， 那么A3就是 ε case ，如果是选中了 action 2 ，那么A3就不是 ε case ，A1与其类似。

2.3 The 10-armed Testbed

粗略评估 greedy 和 ε-greedy 的效率差异：

10-armed testbed ：2000次随机生成的 10-armed bandit problem ，每一次都以标准高斯分布选取10个 $q_\ast (a)$，如下图：

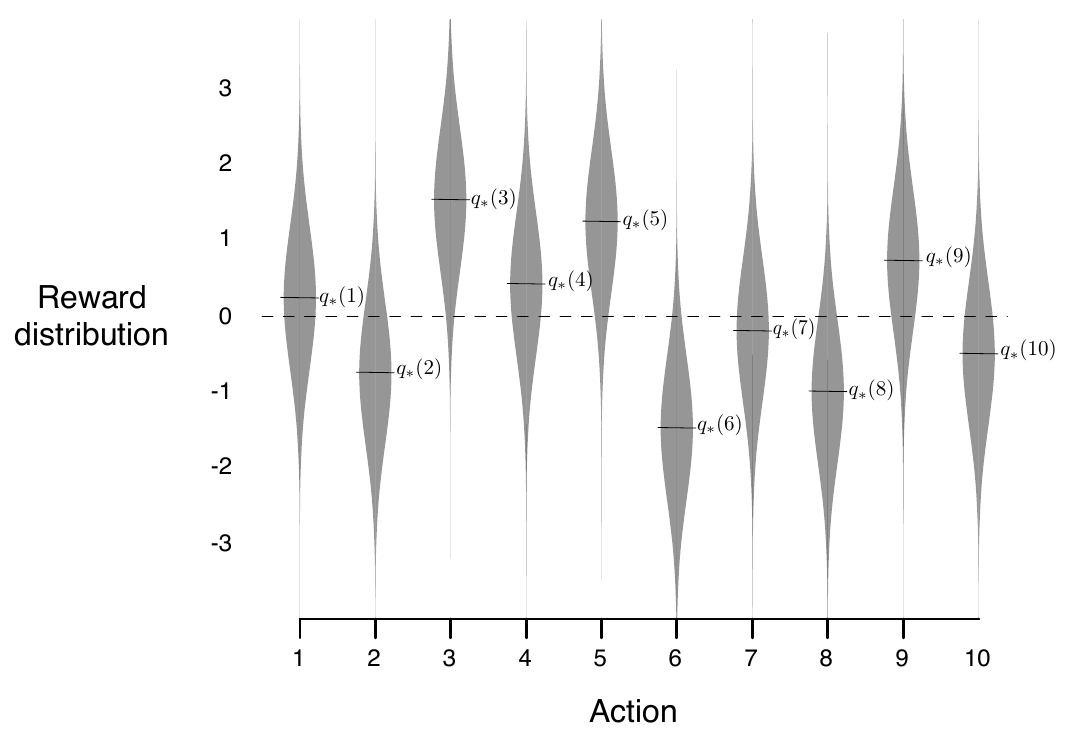
对于每一个 $A_t = a(a = 1, 2,\dots,10)$ 其 reward 都从高斯分布中选取( mean = $q_\ast (a)$， variance = 1) 对于方法的评估：对每一个 10-armed bandit problem ，在经过 1000 time steps 后，称为一轮 run ，经过独立的2000轮次后(不同 10-armed bandit problem )，得到的结果作为该方法的性能评估

结果如下：

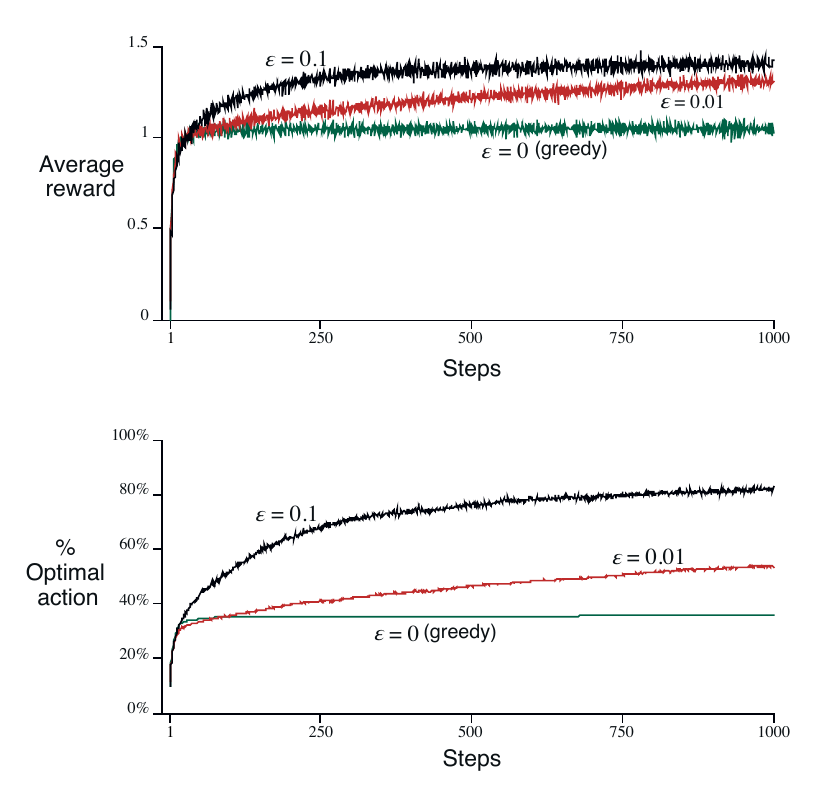
结论：

• 这张图的初始Q值是直接设置为 0 的，如果用 $Q_1(a)$ 作初值的话， optimal action 都会很快达到 $80\%$ 左右
• greedy method 在最开始时会略微地比 $\epsilon$-greedy method 快一丢丢，但是很快收敛于低水平，其 average reward 约为1，其选中最优 action 的次数大约是三分之一，表示其得到了较次的策略

对于 $\epsilon$-greedy method

• $\epsilon = 0.1$ 时，其进步较快，收敛也较快，最终 optimal action 选取率收敛于 $90\%$ 左右
• $\epsilon = 0.01$ 时，进步稍慢，收敛也稍慢，但最终表现会好过 $\epsilon = 0.1$ 的情况，理论上其最终 optimal action 选取率应为 $99\%$，糟糕的是，图上并没有显示出 $\epsilon = 0.01$ 最终的情况
• $\epsilon$-greedy method 取决于具体的任务情况，一般来说， reward 的方差大时， $\epsilon$-greedy method 会更好，如果方差为 0 ，那 $\epsilon$-greedy method 就是在单纯地做无用功

Exercise：

2.3 ： $\epsilon = 0.01$ 的情况会表现最好，假设在足够长的时间后，$\epsilon = 0.1$ 和 $\epsilon = 0.01$ 都找到了最优策略，那么前者会以 $90\%$ 的概率选择 Optimal action ， 而后者会以 $99\%$ 的概率选择 Optimal action ，那么显然后者带来的累计奖励更高。

2.4 Incremental Implementation

action-value methods 总是用 sample-average 来估计 values ，接下来讨论如何有效率地计算 average

针对一个 action $a$ ，令 $R_i$ 为第 $i$ 次选择 $a$ 所得的 reward ，令 $Q_n$ 为 选择 $n - 1$ 次 $a$ 后，对 $a$ 的 value 值的估计，则：

显然，不能保存下每一个 $R_i$，每次都累加计算，时间空间效率都太低，均达到了$O(n)$

显然，$Q_{n+1}$ 可以由 $Q_n$ 、$n$ 与 $R_n$ 三者计算得到 ，时间空间效率都能达到 $O(1)$ ；当然，也可以保存所有 $R$ 的累计和，但是该值会随时间增大，在 $t$ 没有极限的情况下，其有溢出的可能

上式的一般形式如下：

$NewEstimate \leftarrow OldEstimate + StepSize\ [\ Target - OldEstimate\ ]\ .$

其中 $\ [\ Target - OldEstimate\ ]$ 视作估计误差，在估计值不断接近 $Target$ 的过程中随之减小，$StepSize$ 用于随 step 变化实现 Incremental Implementation ，后面写作 $\alpha$

最后，对于 bandit problem 的简单算法如下：

2.5 Tracking a Nonstationary Problem

Nonstationary Problem ： reward probabilities 不是一成不变的，而是会随时间或其它量产生变化

这种情况下，应该给最新的 reward 以高的权重，一般会改变 $\alpha$ 的值来做到这点： $Q_{n+1}\doteq Q_n+\alpha \Big[R_n-Q_n\Big]$ ，该 $\alpha$ 在前面的算法中，表现为 $1/n$ ，$\alpha \in (0, 1]$ ，$\alpha$ 越大，表示越看重新的 reward ；$\alpha$ 越小，则表明越看重之前已得到的估计。

上式表明，$i$ 越小，也就是越靠前的 $R_i$，其权重越小，因为$1-\alpha<1$; 极端情况下，即$1 - \alpha = 0$，则上式写作：$Q_{n+1} = R_n$， 这种表达称作加权平均 weighted average ，因为有：

reward 的权重以 $1 - \alpha$ 的比例呈指数性衰减，这有时被称作 exponential recency-weighted average

令 $\alpha_n(a)$ 为第 $n$ 次选择 action $a$ 时所用的 step-size parameter 。在之前的学习中，$\alpha_n(a)= 1/n$ ，这能让$Q_n$ 收敛。

但是很显然，并不是所有的 $\alpha_n(a)$ 都能让$Q_n$ 收敛，比如 $\alpha_n(a)=0.5$ 就不行。

在随机逼近理论(stochastic approximation)中，给出了保证收敛的条件：

前一个条件用于保证 steps 足够大，以排除任何初始条件或随机扰动的干扰；后一个条件保证了收敛性。

在后面的案例中，第二个条件将得不到满足，这使得 $Q_n$ 不会最终收敛于定值，而是始终受到 $R_n$ 的影响，但正如之前所提到的，在非稳定的环境中，这正是我们所需要的。

另外，满足两个条件的 $\alpha_n(a)$ 往往收敛得很慢，或者需要精心调整参数以得到一个令人满意的收敛速度。因此，这两个条件通常只用在理论工作中，在实际应用和研究中很少使用。

Exercise：

2.4：当 $\alpha$ 不为常数时，$Q_{n+1}$ 与 $R_1$~$R_n$ 的关系可表示如下：

2.5：编程题：设计并实现一个实验，用来观察在非稳定环境下 sample-average methods 的缺点。

使用 10-armed testbed 的变种：所有的初始 $q_\ast (a)$ 都相等，并且每一步都分别为每一个 $q_\ast (a)$ 额外加上一个取自高斯分布的变化 ( $mean = 0\ and\ variance = 0.1$ )

使用两个方法对比： sample-average 以及 $constant\ \alpha = 0.1$；设 $\epsilon = 0.1$；画出如 2.2 的图像

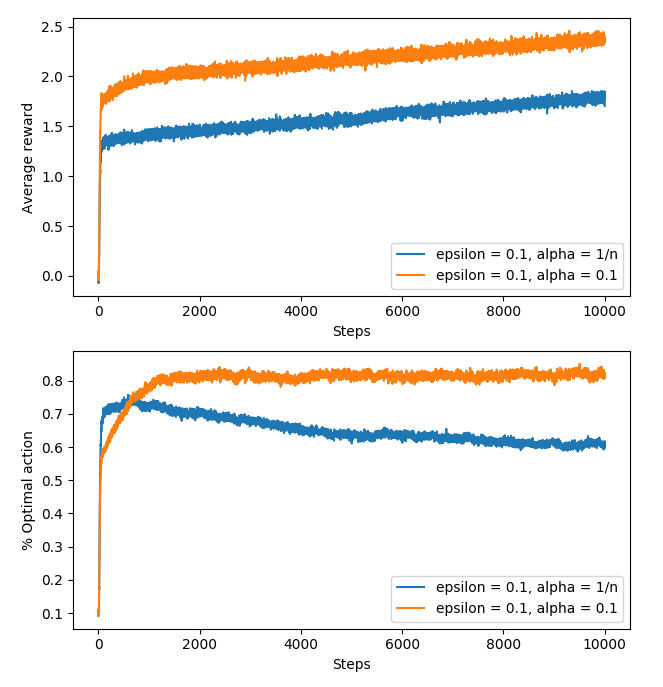
结果如下图，看得出来， sample-average methods 明显劣于 constant $\alpha$

这是因为 sample-average 在 $n$ 稍大后，其 $Q$ 函数便会很快收敛，而由于环境是 nonstationary ，所以收敛的 $Q$ 函数不适用于新的环境了

而 constant $\alpha$ 中 ，新的 reward 会起到较重的作用，且 $Q$ 函数一般不收敛，所以能够跟着环境做调整

2.6 Optimistic Initial Values

前面的方法中，初始化的方法为 $Q_1(a)$，即先为每一个 $a$ 运行一次，得到其 reward 作为初始 $Q$ 值，这会给 $Q$ 函数带来偏差 bias

在 sample-average methods 中，这个偏差会很快消失；而在 constant α 中，会随着时间减小

而在实际应用中，这个偏差通常不会带来麻烦，反而在有些时候大有好处

缺点是，该参数成了一组需要人为用心挑选的参数，即使只是全设成 $0$ ；而优点则是它能很方便地一些关于所期望的奖励水平的先验知识

初始 $Q$ 值也可以方便地用于鼓励 explore ，比如把上面的 10-armed bandit problems 的 $Q_1(a)$ 全部设成 $+5$ ，那么在开始的时候，算法总是会得到低于 $5$ 的 reward ，$Q$ 值被更新成较小的值，那么算法就会去尝试其它的 action ，而被选中的 action 的 $Q$ 值总是被减少，也就是说 greedy-action 会不停地变化；反复如此，便能轻松地起到鼓励 explore 的作用；而在 $n$ 稍大一些时， $+5$ 的副作用便轻松的被消去了。

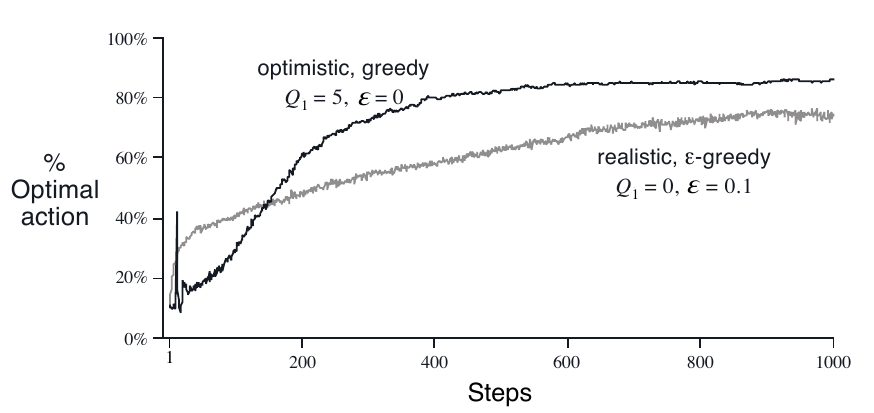
这种鼓励 explore 的方法称作 optimistic initial values ， 在 stationary problems 可作为提高效率的小技巧

但是，在 nonstationary problems 中并不适用，因为它鼓励 explore 的作用持续很短，只要 $n$ 稍大些，初值的效果便会被消去 事实上，在一般的 nonstationary case 中，任何关于初始条件的方法均很难起到作用，包括 sample-average methods ，它也将初值视作一个特殊值，因为它对所有 rewards 的权重都是相等的。

Exercise：

2.6：Mysterious Spikes：为什么上图中，$Q_1 = 5$ 这条线的前期会有陡峭的振荡，如何优化？

实验发现，陡峭的峰点位于 $step=11$ 处，也就是说，在第11次 action 时，发生了高概率选中 optimal action 的情况；

这是因为，在前面10(本例中，$k=10$ )次选择中，没被选过的 action 的 $Q$ 值为 $5$ ，而所有被选中的 action 的 $Q$ 值都会被减小；所以前10次选择的结果都是遍历 $k$ 个 action ，因此1-10次选中 optimal action 的概率都是 $10\%$；而到了第11次选择时，因为经过了一遍遍历， optimal action 的估计值会比 non-optimal action 的估计值要以较大的概率(约 $43\%$ )高出一些，所以会增加中选概率;第12,13,14次选择都有类似的情况。而到了 14 以后， optimal action 的优势又被随机量给覆盖了(多次选择后， optimal action 突出的情况被抹消)，没有了第一次选择的大优势，曲线逐渐恢复平稳。

2.7 Upper-Confidence-Bound Action Selection

之前的 explore 中， $\epsilon$-greedy methods 对于 non-greedy action 是随机选的。

upper confidence bound (UCB) 会根据 non-greedy action 的 greedy 程度来选择：

$N_t(a)$ 是 action $a$ 在 $t$ 时刻前被选过的次数，当其为 $0$ 时视 $a$ 为 greedy-action ，$c > 0$ 控制 exploration 的强度，$c$ 越大， explore 的力度越大

该方法中，平方根中的值表明了 value 估计值的不确定程度或方差；$\arg\max$ 相当于对 action value 的上界 upper bound 做一个排序，$c$ 表明了这个排序的可信度

action $a$ 被选中的次数越多，其不确定性就越小 (分母变小)；相对的，随着 $t$ 的增大，没被选中的那些 action 的不确定度会增大，使用对数表明时间越往后，不确定值的增长越小，但它是无界的

在所有的 action 被选得多了后，那些 $Q$ 值小的、被选中次数多的 action ，会减少被选中的频率

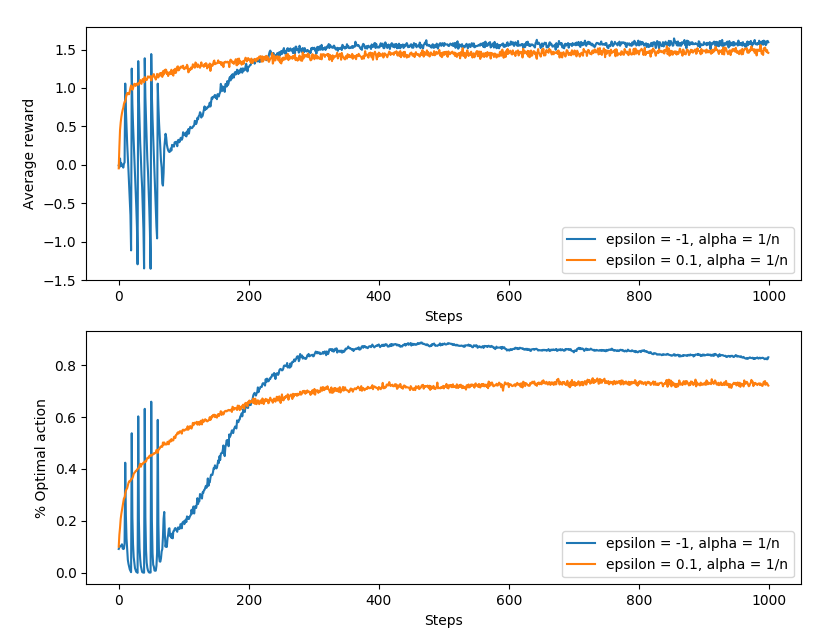
如上图，其中 $\epsilon = -1$ 的即是 UCB ，前面的抖动是在每轮遍历所有 action 后发生的：第一轮选取时，那些 $N_t(a) = 0$ 的视为 greedy-action ，因此前 $k$ 次会遍历所有 action ，到了第 $k+1$ 次时，由于所有的 $N_t(a) = 1$，因此会选中 $Q_t(a)$ 最高的那个，于是大概率选中了 optimal action ；第二轮也是类似的情况，在式中不确定值起到较大的作用，到了都遍历两轮后，便是 $Q_t(a)$ 起到较大作用，多次如此后； $N_t(a)$ 变大，不确定度变小，于是曲线趋于平稳。

UCB 虽然在本例中效果好于 $\epsilon$-greedy ，但是并不如 $\epsilon$-greedy 实用，原因在于其更难扩展到其它普遍的RL 问题中(至少在本书后面的例子中是这样的)
一是不好处理 nonstationary problems ，二是不好处理较大的状态空间，尤其是在用函数逼近的情况下；在这些情况中 UCB 并不实用

2.8 Gradient Bandit Algorithms

之前的方法都是估计一个 action values ，然后用它来选 actions ，本节会用一个 numerical preference — $H_t(a)$ 来选action：

$H_t(a)$ 越大，$a$ 被选中的概率越大，但是无法给出 $H_t(a)$ 与 reward 的关系表达
$H_t(a)$ 的值中，只有不同的 $a$ 之间的差值是有意义的，因此，使用 soft-max distribution 来选择 $a$

$\pi_t(a)$ 表示了在 $t$ 时刻选择 action $a$ 的概率，对于任意的 $a$ ，有：$H_1(a)=0$

Exercise

2.7: 说明：在仅有两个 action 的情况下，使用 soft-max distribution 与使用 logistic(sigmoid) function 是一样的

待做

在这种 随机梯度上升 (stochastic gradient ascent) 的情形中，有一个很直觉的算法，根据每一步选中的 action $A_t$ 和所获得的 reward $R_t$ 更新所有 $H_{t+1}(a)$ :

其中， $\bar R_t\in \Bbb R$ 在 $t$ (包含)时刻以前，所有 rewards 的平均值，它作为一个 baseline 与其它 rewards 作比较。如果新的 reward 高于它，就提高 $A_t$ 的被选几率；反之则降低。 未选中的 actions 与被选中的 action 操作相反。

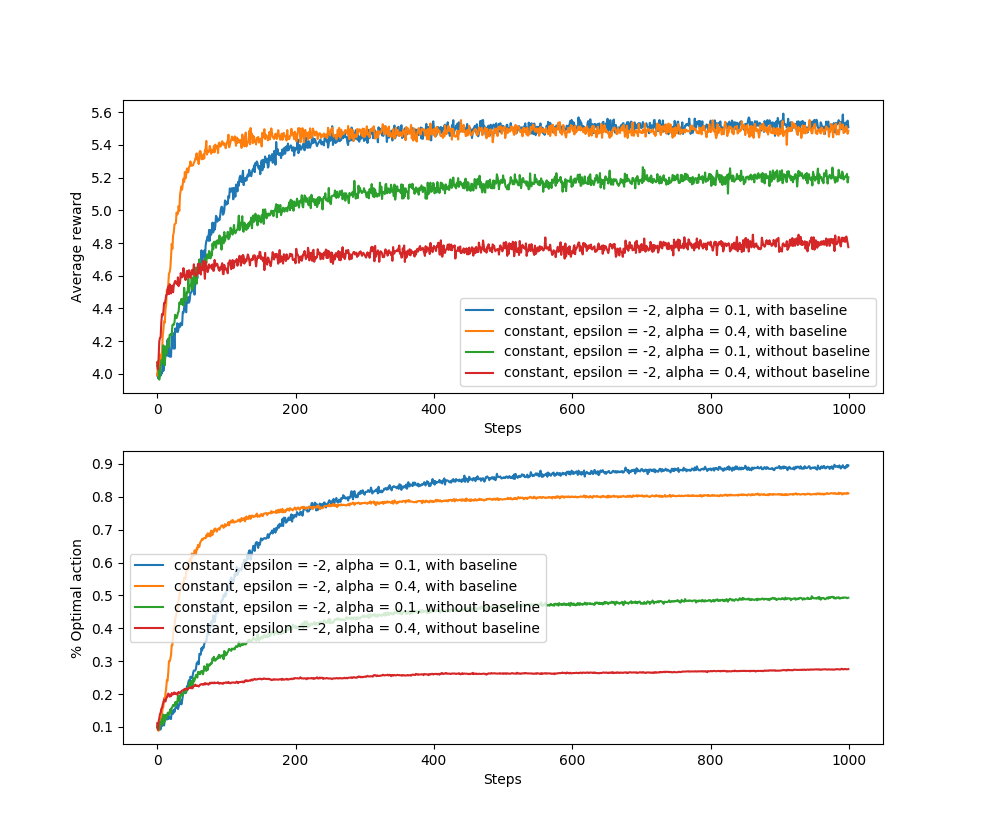
接下来验证上述算法是梯度上升的一种形式：

标准梯度上升的形式如下：

其中 $\Bbb E[R_t]=\sum_x\pi_t(x)q_\ast (x)$ ,虽然 $q_\ast (x)$ 并不完全可知，但是其期望值与我们接下来在式中所用的是相等的

其中 $B_t$ 即为 baseline ，其与 $x$ 无关。因为 $\sum_x\frac {\partial \pi_t(x)}{\partial H_t(a)}=0$ ，因此，加入 $B_t$ 并不会改变等式。

接下来分式上下同乘 $\pi_t(x)$ ，就得到了期望的形式：

$\begin{align} \frac {\partial \Bbb E[R_t]}{\partial H_t(a)} & = \sum_x\pi_t(x)\big(q_\ast (x)-B_t\big) \frac {\partial \pi_t(x)}{\partial H_t(a)}/\pi_t(x) \\ &= \Bbb E\bigg[\big(q_\ast (A_t)-B_t\big)\frac {\partial \pi_t(A_t)}{\partial H_t(a)}/\pi_t(A_t)\bigg] \\ &= \Bbb E\bigg[\big(R_t-\bar R_t\big)\frac {\partial \pi_t(A_t)}{\partial H_t(a)}/\pi_t(A_t)\bigg] \\ & = \Bbb E\Big[\big(R_t-\bar R_t\big)\pi_t(A_t)\big(\Bbb I_{a=A_t}-\pi_t(a)\big)/\pi_t(A_t)\Big] \qquad \text{(下面证明)}\\ & = \Bbb E\Big[\big(R_t-\bar R_t\big)\big(\Bbb I_{a=A_t}-\pi_t(a)\big)\Big] \end{align}$
令 $B_t = \bar R_t$ ，因为 $\Bbb E[R_t|A_t]=q_\ast (A_t)$，所以可以将 $q_\ast (A_t)$ 替换成 $R_t$ ， 就得到了算法中所用的更新公式：

下面证明 $\frac {\partial \pi_t(x)}{\partial H_t(a)}=\pi_t(x)\big(\Bbb I_{a=x}-\pi_t(a)\big)$ , 其中 $\Bbb I_{a=x}$ 在 $a=x$ 时为 $1$ ，在$a\neq x$ 时为 $0$ :

首先引出分式的偏导数的标准形式：

利用该式，做以下推导：

证毕

随机梯度上升能够保证算法具有鲁棒的收敛性

注意：算法的更新不依赖于所选的动作 action ，也不依赖于奖励基线 baseline ， baseline 的取值不会影响更新的结果，不过会影响到更新收敛的速度。因为梯度的期望不受 baseline 的影响，但梯度的方差受到了影响。

2.9 Associative Search (Contextual Bandits)

之前讨论的是 nonassociative tasks ，也即不需要建立状态与动作之间的联系，接下来将讨论 associative task ，需要建立从状态到最优动作之间的映射关系。

举个例子：一个新的老虎机问题：现在我们需要在 10 个老虎机问题中进行决策，这10组老虎机的 $q_\ast (a)$ 各不相同，每次随机选择一组老虎机进行选择，如果不知道或者不使用老虎机组合的编号，那么上面的方法将起不到任何作用。只有将老虎机组合的编号用上，为每组老虎机考虑不同的 action ，才能得到理想的奖励。这就是为老虎机组合的状态(编号)与对应的动作之间建立起映射关系。

Associative search taks 常被叫做 contextual bandits ，其介于简单的 k-armed banditproblem 和完全的RL问题之间，它虽然建立了状态与动作的联系，但是动作还是只影响到立即奖励，而不影响后续状态。

Exercise

2.8：如果不知道是哪一个 case ，那么无论怎么选，动作 1 和动作 2 的期望奖励都是 $0.5$ 。 而如果知道是哪一个 case ，那么在学习到 case 与 action value 之间的映射后，就能总是选到 value 更高的 action ，那么期望奖励能够达到 $0.55$

2.10 Summary

本章介绍了权衡 exploration 和 exploitation 的几个简单方法。

• $\epsilon$ methods 是以小概率随机选取 non-greedy action
• UCB methods 则是会在 explore 时偏向那些样本较少的 action 。当然，这是以 value 为基准的
• Gradient 并不估计 action values ，而是 action preferences ，
• 简单的初始化可以让算法有效地进行 explore

以上方法在 10-armed testbed 中的性能表现如下图：

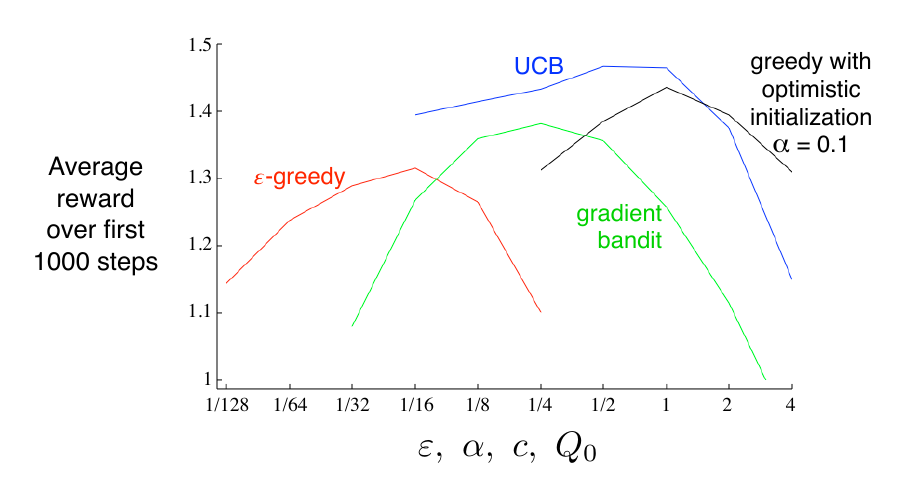
这些方法的性能都受到参数的影响，我们在考虑方法的性能时，不仅要考虑其在最优参数处表现出的性能，还要考虑方法本身对参数的敏感性。如果方法足够敏感，调参会方便些，但如果太过敏感，也许又会使其失去泛化能力和可重复性。

• 在 k-armed bandit problems 中，平衡 exploration 和 exploitation 的最有方法是 Gittins indices ，但它假设了可能问题的先验分布是已知的，而这无论在理论上还是在计算易处理性上都不能推广到完全的RL问题中。

• 贝叶斯方法假定了 action values 的一个已知的初始分布。一般来说，其更新的计算过程会非常复杂，除了某些特定的分布外( conjugate priors )，一个可能的办法是在每一步根据可能是最优动作的后验概率来选择 action 。该方法常被叫做 posterior sampling 或 Thompson sampling.

• 贝叶斯方法可想见能够达到 exploration 和 exploitation 的最优平衡。能够为所有的动作计算可能得到的立即奖励、导致的后验分布与动作值的关系。但是它的状态空间增长得太快，几乎不可能完成如此巨大的计算量，但是逼近它是有可能的。

Exercise

2.9 (programming): 给出一张类似图2.6的图，基于 Exercise 2.5 ， non-stationary case ，$\epsilon$-greedy method , $\alpha=0.1$ ，每轮 $200,000$ 步，对于每一种算法-参数组，使用后 $100,000$ 步的平均奖励作为数据。

待做